![[image]](img/mechsystem1.gif)
MechSystem. The source code of the Lagrange
Applet is in the file Lagrange.java. This is where the
individual mechanical systems, such as SpringPendulum, are defined.
You can edit this file to implement other mechanical systems. This
document describes how to write the code to do so.
Fortunately, the pre-defined class MechSystem already
implements all the gory details of Lagrangian mechanics and the actual
simulation. To define your own mechanical system, you only need to
provide information that describes the physics of the particular
system that you want to simulate. There are three groups of methods
that need to be defined:
In the methods that you will define, all the calculations are done in
actual physical units, such as meters and kilograms, and not in
computer units, such as pixels. The relevant conversions to screen
coordinates etc. are automatically handeled by the superclass
MechSystem. This way, you only need to worry about the
physical properties of the mechanical system you are defining.
Let m0 and m1 be the inner and outer mass, respectively. Let l0 and l1 be the length of the inner and outer leg, where l0 is the length of the spring in its relaxed state. Let k0 be the spring constant. Masses are measured in kilograms, lengths in meters, and spring constants in Newton/meter. Also, let g=9.81m/s2 be the gravitational constant. The system has three coordinates: x and y are the coordinates of the first mass, measured in meters in a coordinate system that has the pivot point as its origin. Alpha is the angle of the outer leg, measured in radians counterclockwise from south. We number the coordinates: q0=x, q1=y, q2=alpha.
The kinetic and potential energy of the spring pendulum are given by:
class SpringPendulum extends MechSystem {
private double m0, m1, l0, l1, k0, g; // physical parameters private int rad0, rad1; // radii of massesNext, we need to define three methods that provide general information about the system. The method
getType() simply returns the name
of this class.
String getType() {
return "SpringPendulum";
}
The method getParamInfo() returns information about the
physical parameters. In the case of the spring pendulum, there are six
parameters. The method returns an array of objects of type
Parameter. Each entry describes one parameter, by giving
its name, brief description, physical units, and default value.
Parameter[] getParamInfo() {
Parameter[] paraminfo = {
new Parameter("m0", "inner mass", "kg", 2),
new Parameter("m1", "outer mass", "kg", 1),
new Parameter("l0", "inner length", "m", 6),
new Parameter("l1", "outer length", "m", 4),
new Parameter("k0", "spring constant", "N/m", 60),
new Parameter("g", "gravity", "m/s^2", 9.81),
};
return paraminfo;
}
The method getCoordInfo() returns information about the
coordinates. In this case, there are three coordinates: x, y, and alpha.
The method returns an array of objects of type Coordinate.
Each entry describes one coordinate, by giving its name, a brief
description, physical units, default initial value, default initial value
of the derivative, and the period of this coordinate. For instance, the
period of the coordinate alpha is 2pi. The coordinates x and y are not
periodic, so the period is set to 0.
Coordinate[] getCoordInfo() {
Coordinate[] coordinfo = {
new Coordinate("x", "coordinate of inner mass, right of pivot", "m",
2.2, 0, 0),
new Coordinate("y", "coordinate of inner mass, above pivot", "m",
3, 0, 0),
new Coordinate("alpha",
"angle of outer leg, counterclockwise from south",
"radians", 4, 0, 2*Math.PI),
};
return coordinfo;
}
The method setphysics() is used to set the internal variables
that depend on physical parameters, such as m0, m1, etc. It is called
during initialization, and also each time one of the parameters changes.
The values of the parameters are passed in a double array
param. The parameters appear in this array in the order in
which getParamInfo() declares them. This is also the place to
set any other internal variables that depend on the parameters, such as the
radii of the two masses in this example.
void setphysics(double[] param) {
m0=param[0];
m1=param[1];
l0=param[2];
l1=param[3];
k0=param[4];
g =param[5];
rad0 = (int)(5*Math.sqrt(m0/Math.max(m0,m1)));
rad1 = (int)(5*Math.sqrt(m1/Math.max(m0,m1)));
}
double arrays q, respectively,
qp. The method sq(double), defined in the class
MechSystem, may be used for squaring a value.
The simulation of the Lagrange Applet has preservation of energy built-in, so that the system does not spin out of control as easily in the face of numerical errors. For that reason, neither the potential nor the kinetic energy are allowed to have an explicit time dependency. Also, the algorithm used to adjust the total energy uses the fact that the kinetic energy depends quadratically on the first derivatives of the coordinates, and it is likely to fail if the kinetic energy does not have this property. (However, forced preservation of energy can also be turned off).
// kinetic energy
double T(double q[], double qp[]) {
return (m0+m1)/2 * (sq(qp[0])+sq(qp[1]))
+ m1/2 * sq(l1)*sq(qp[2])
+ m1 * qp[2]*l1*(qp[0]*Math.cos(q[2])+qp[1]*Math.sin(q[2]));
}
// potential energy
double U(double q[]) {
return k0/2 * sq(Math.sqrt(sq(q[0])+sq(q[1]))-l0)
+ (m0+m1)*g * q[1]
- m1*g * l1*Math.cos(q[2]);
}
The superclass MechSystem defines three methods
diffq(int i, double q[], double qp[]), diffpp(int
i, int j, double q[], double qp[]), and diffqp(int i, int
j, double q[], double qp[]) that use a numerical method to
calculate the respective partial derivatives (where L = T - U):
If you wish, you may override these with methods that calculate the relevant partial derivatives using an exact formula; this will slightly enhance performance.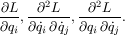
drawsystem() draws the current
state. For this purpose, it may call the methods drawSpring(),
drawLine(), drawMass(),
drawCircle(), and recordTrace(), all of which are
provided by the superclass MechSystem. These methods expect
physical coordinates (in meters); conversions to screen coordinates are
taken care of by the superclass.
The recordtrace method must be invoked to draw a trace
segment; this is drawn on the background bg as well as on the
foreground og.
The method drawsystem() may also invoke arbitrary drawing
methods on the Graphics object og; however, in this case, the
coordinates must be converted explicitly, for instance
og.drawRectangle(c.x(left), c.y(top), c.dx(right-left),
c.dy(bot-top)). The methods c.x() and
c.y() convert physical coordinates to screen coordinates, and
the methods c.dx() and c.dy() convert
differences of physical coordinates to differences of screen
coordinates. Note that in the physical coordinate system, the y-axis points
upwards. Before invoking a drawing method of og, the correct
color must be set with og.setColor(Global.fgcolor).
void drawsystem(Graphics og, Graphics bg) {
double x0 = q[0];
double y0 = q[1];
double x1 = x0+l1*Math.sin(q[2]);
double y1 = y0-l1*Math.cos(q[2]);
recordTrace(bg,og,x1,y1);
drawSpring(og,0,0,x0,y0,15,0.2);
drawLine(og,x0,y0,x1,y1);
drawMass(og,x0,y0,rad0);
drawMass(og,x1,y1,rad1);
}
The method bounds() is used to determine the size of the
image that drawsystem() is going to draw. It returns a
rectangle of physical coordinates that represents upper and lower
bounds on the coordinates used by the drawing methods in
drawsystem(). It is important that this rectangle is big
enough to draw not just the current state, but also future states that
may arise as the system evolves. Conservation of energy may be
assumed for this purpose; should the energy change, the method
bounds() is called again. The method E() can
be called to calculate the current total energy of the system. The
result should be returned with the statement return new
DoubleRectangle(left,bot,right,top).enlarge(.05), where the
enlarge() method on a rectangle adds a little space
around the edges.
DoubleRectangle bounds() {
double l=l1+l0+
Math.sqrt(sq((m0+m1)*g/k0)+2*l0*(m0+m1)*g/k0+2*m1*g/k0+2*E()/k0);
double equi=(m0+m1)*g/k0;
return new DoubleRectangle(-l,-equi-l,l,-equi+l).enlarge(.05);
}
mouseMap() maps (x,y)-coordinates to
internal coordinates for the purpose of mouse action. It should contain a
sequence of statements of the form map(i,v), which means set
the ith coordinate to the value v. In the case of our spring pendulum, the
definition of mouseMap() is simply this:
void mouseMap(double x, double y) {
map(0, x);
map(1, y);
}
This means that when the mouse is clicked on coordinates (x,y), then the
coordinate q0 of the dynamical systems is fixed to x and the
coordinate q1 is fixed to y. If we had some other mechanical
system, where the coordinate q0 denoted some angle, measured
counterclockwise from south, we would define
void mouseMap(double x, double y) {
map(0, Math.atan2(x,-y));
}
The default implementation of mouseMap does nothing; so if it
is not overridden, then mouse clicks and drags will have no effect. This
finishes the definition of the class SpringPendulum.
(new DoublePendulum()).appendInfoVector(infov);
(new DoubleSpring()).appendInfoVector(infov);
(new SpringPendulum()).appendInfoVector(infov);
// *** add your own system here ***
...
if (type.equals("doublependulum")) {
mechsys = new DoublePendulum();
} else if (type.equals("springpendulum")) {
mechsys = new SpringPendulum();
} else if (type.equals("doublespring")) {
mechsys = new DoubleSpring();
// *** add your own system here ***
This is it. Have fun designing your own mechanical systems!
Back to main Lagrange page.
Back to Peter Selinger's Homepage:
![]()