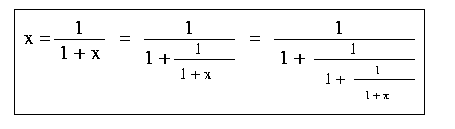A Deeper Look at Fibonacci Numbers

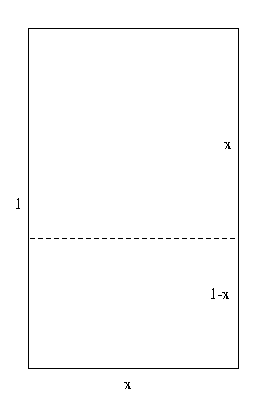
Here is an interesting way to use the Fibonacci numbers to build up a pleasing rectangle and spiral: Try this on graph paper. The successive rectangles generated in the exercise above look more and more like the golden rectangle as you add additional squares. The requirement for this "golden rectangle" of ancient Greek architechture and the great painters of the Rčnaissance is that the big rectangle must be similar (in proportions) to the smaller rectangle inside. Thus, x/1 = (1 - x)/x This implies x2 = 1 - x Hence x2 + x - 1 = 0      (*) Or x = 1/(1 + x)      (**) The equation (*) has roots (-1 + Ö5)/2 and (-1 - Ö5)/2. Since x must be positive, we take x = (-1 + Ö5)/2 = (Ö5 - 1)/2 ~ 0.6180339887498948482046... x = 1/(1 + x)      (**) There is interesting information in (**) as well. 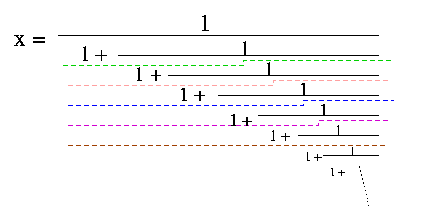If the expression for x in (**) is plugged into the right hand side and this step is repeated we get If this is continued indefinitely, we get a continued fraction expression for x. (Ignore the coloured dashed lines at first.) If you cut this off at the green line, the fraction simplifies to 1/2. If you cut this off at the pink line, the fraction simplifies to 2/3. If you cut this off at the blue line, the fraction simplifies to 3/5. If you cut this off at the magenta line, the fraction simplifies to 5/8. If you cut this off at the brown line, the fraction simplifies to 8/13. And so on.... As a distinctive notation, we will use f to denote the golden ratio. Thus, f = (Ö5 - 1)/2 ~ 0.6180339887498948482046...