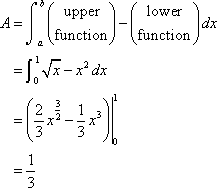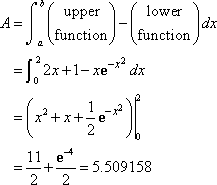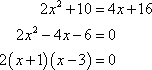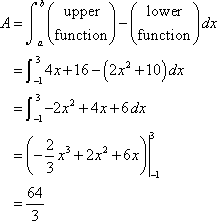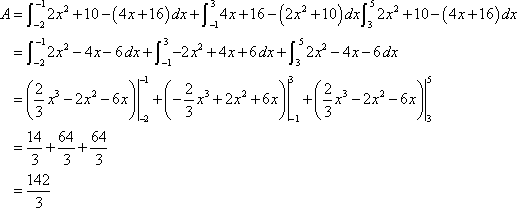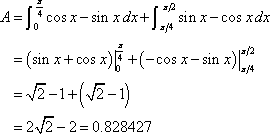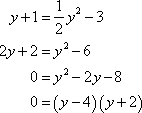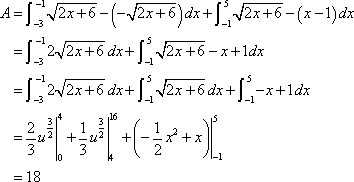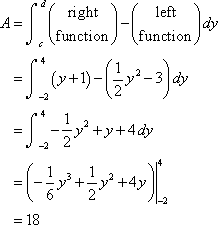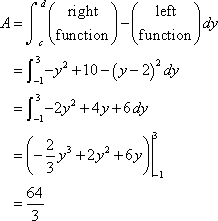Area Between Curves
In this section we are going to look at finding the area between two curves.There are actually two cases that we are going to be looking at.
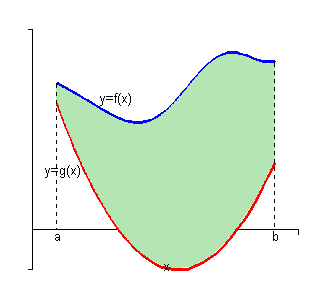
In the first case we are want to determine the area between y=f(x) and y=g(x) on the interval [a,b]. We are also going to assume that ![]()
|
|
|
In the final section of the Extras chapter we derived the following formula for the area in this case.
|
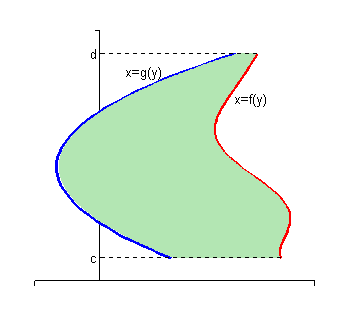
The second case is almost identical to the first case. Here we are going to determine the area between x=f(y) and x=g(y) on the interval [c,d] with
![]() .
.
|
In this case the formula is,
|
Now (1) and (2) are perfectly serviceable formulas, however, it is sometimes easy to forget that these always require the first function to be the larger of the two functions. So, instead of these formulas we will instead use the following formulas.
In the first case we will use,
|
(3) |
In the second case we will use,
|
(4) |
Using these formulas will always force us to think about what is going on with each problem.
Let¡¯s work an example.
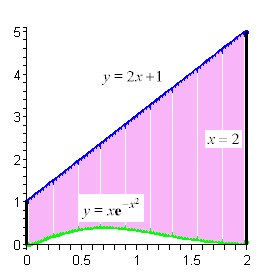
Example 1 Determine the area of the region enclosed by
![]() and
and ![]() .
.
Solution
First of all, just what do we mean by ¡°area enclosed by¡±. This means that the region must have one of the two curves on every boundary of the region.
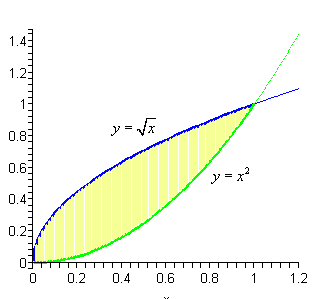
So, to determine what this region is, it will be best to graph the two functions. Also notice that we are going to have to determine which of the two functions is the larger of the two and if you think about it that is not clear with these two functions.
So, here is a graph of the two functions with the enclosed region shaded.
|
|
|
The enclosed region is the yellow shaded region in the graph. Note that we don¡¯t take any part of the region to the right of the intersection point of these two graphs. In this region there is no boundary on the right side and so is not part of the enclosed area. Remember that one of the given functions must be on the each boundary of the enclosed region.
Also from this graph it¡¯s clear that the upper function will be dependent on the range of x¡¯s that we use. Because of this you should always sketch of a graph of the region. Without a sketch it¡¯s often easy to mistake which of the two functions is the larger. In this case most would probably say that
![]() is the upper function and they would be right for the vast majority of the x¡¯s. However, in this case it is the lower of the two functions.
is the upper function and they would be right for the vast majority of the x¡¯s. However, in this case it is the lower of the two functions.
The limits of integration for this will be the intersection points of the two curves. In this case it¡¯s pretty easy to see that they will intersect at x=0 and x=1 so these are the limits of integration.
So, the integral that we¡¯ll need to compute to find the area is,
|
Before moving on to the next example, there are a couple of important things to note.
First, in almost all of these problems a graph is almost required. Often the bounding region, which will give the limits of integration, is difficult to determine without a graph.
Also, it can often be difficult to determine which of the functions is the upper function and with is the lower function without a graph. This is especially true in cases like the last example where the answer to that question actually depended upon the range of x¡¯s that we were using.
Finally, unlike the area under a curve that we looked at in the previous chapter the area between two curves will always be positive. If we get a negative number or zero we can be sure that we¡¯ve made a mistake somewhere and will need to go back and find it.
Note as well that sometimes instead of saying region enclosed by we will say region bounded by. They mean the same thing.
Let¡¯s work some more examples.
Example 2 Determine the area of the region enclosed by
![]() ,
,
![]() ,
,
![]() , and the y-axis.
, and the y-axis.
Solution
In this case the last two pieces of information (
![]() and the y-axis) tell us where to stop the region. Here is the graph with the enclosed region shaded in.
and the y-axis) tell us where to stop the region. Here is the graph with the enclosed region shaded in.
|
|
Here, unlike the first example, the two curves don¡¯t meet. Instead we rely on two vertical lines to bound the left and right sides of the region.
Here is the integral that will give the area.
|
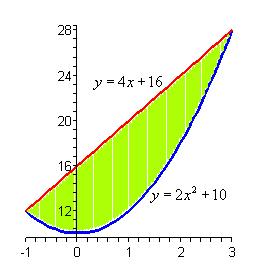
Example 3 Determine the area of the region bounded by
![]() and
and
![]() .
.
Solution
In this case the intersection points (which we¡¯ll need eventually) are not going to be easily found from the graph so let¡¯s go a head and get them now. In this case we can get the intersection points by setting the two equations equal.
|
So it looks like the two curves will intersect at x=-1 and x=3. If we need them we can get the y values corresponding to each of these by plugging the values back into either of the equations. Note that if you aren¡¯t good at graphing these points can help somewhat in getting the graph. We now know two points that are on the graph (-1,12) and (3,28). These will give us a place to start the graph.
Here is a graph of the region.
|
|
|
With the graph we can now identify the upper and lower function and so we can now find the enclosed area.
|
Be careful with parenthesis in these problems. One of the more common mistakes students make with these problems is to neglect parenthesis on the second term.
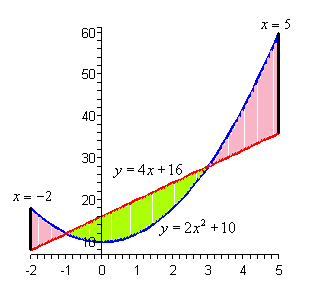
Example 4 Determine the area of the region bounded by
![]() ,
,
![]() ,
,
![]() and
and
![]()
Solution
So, the functions used in this problem are identical to the functions from the first problem. The difference is that we¡¯ve extended the bounded region out from the intersection points.
Here is a graph of this region.
|
Okay, we have a small problem here. Our formula requires that one function always be the upper function and the other function always be the lower function. The actually isn¡¯t the problem that it might at first appear to be. All that we need to do is find the area of each of the three regions, which we can do, and then add them all up.
Here is the area.
|
|
|
|
Example 5 Determine the area of the region enclosed by
Solution First let¡¯s get a graph of the region.
So, we have another situation where we will need to do two integrals to get the area. The intersection point will be where
in the interval. This will be
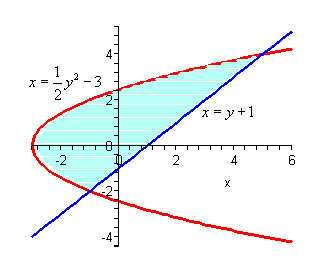
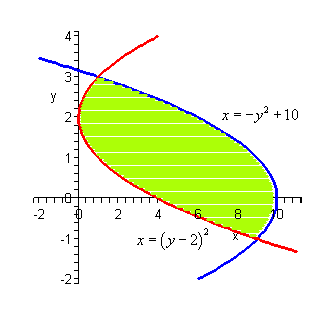
We will need to be careful with this next example. Example 6 Determine the area of the region enclosed by
Solution Don¡¯t let the first equation get you upset. We will have to deal with these kinds of equations occasionally so we¡¯ll need to get used to dealing with them. First we will need intersection points for the two curves. In this case we¡¯ll get the intersection points by solving the second equation for x and the setting them equal.
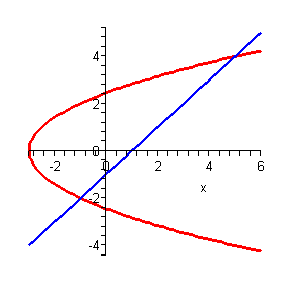
So, it looks like the two curves will intersect at y=-2 and y=4 or if we need the full coordinates they will be : (-1,-2) and (5,4). Here is a sketch of the two curves.
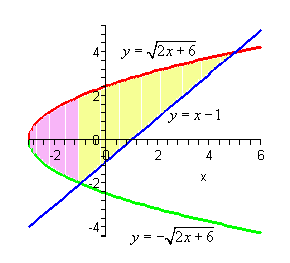
Now, we have a serious problem at this point if we aren¡¯t careful. To this point we¡¯ve been using an upper function and a lower function. To do that here notice that there are actually two portions of the region that will have different lower functions. In the range [-2,-1] the parabola is actually both the upper and the lower function. To use the formula that we¡¯ve been using to this point we need to solve the parabola for y. This gives,
where the ¡°+¡± gives the upper portion of the parabola and the ¡°-¡± gives the lower portion. Here is a sketch of the region if we were going to use the first formula.
The integrals for the area would then be,
While these integrals aren¡¯t terribly difficult they are more difficult than they need to be. Recall that there is another formula for determining the area. It is,
and in our case we do have one function that is always on the left and the other is always on the right. So, in this case this is definitely the way to go. Note that we will need to rewrite the equation of the line since it will need to be in the form
In this case the area is,
This is the same that we got using the first formula and this was definitely easier than the first method. So, in this last example we¡¯ve seen a case where we could use either formula to find the area. However, the second was definitely easier. Students often come into a calculus class with the idea that the only easy way to work with functions is to use them in the form y=f(x). However, as we¡¯ve seen in this previous example there are definitely times when it will be easier to work with functions in the form x=f(y). Make sure that you can deal with them in this form. Let¡¯s take a look at one more example of this. Example 7 Determine the area of the region bounded by
Solution First, we will need intersection points.
The intersection points are y=-1 and y=3. Here is a sketch of the region.
This is definitely a region where the second area formula will be easier. If we used the first there would be three different regions that we¡¯d have to look at. The area in this case is,
|