 (1)
(1) This is a conservative system and generic initial positions result in chaotic dynamics. For example, consider 25 vortices initially located on a ring, with γj=1/25. The movie on the right shows the resulting dynamics. Note that the ring eventually breaks up due to an instability and the result is chaos.
Chaos in (1)
Stable relative equilibrium of (1)
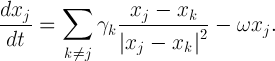 (2)
(2) Here, ω is the angular velocity. There is a one-to-one correspondence between the steady statates xj(t) = ξj of (2) and the relative equilibrium zj(t) = exp(iω t)ξj of (1). More importantly, the relative equilibrium for the vortex model (1) is stable if and only if the corresponding steady state for the swarm model (2) is asymptotically stable. The movie on the right shows the evolution of a ring towards the stable lattice equilibrium using the swarming model.
Swarming model (2)
 (3)
(3) Here, the μ term models damping. The advantage of this formulation is that any relative equilibrium of (3) is automatically a relative equilibrium of (1). Moreover the relative equilibrium of (3) is stable for any mu>0 if and only if it is stable (neutrally, in Hamiltonian sense) for (1). For example, the movie to the right shows the simulation with μ=0.1, with initial conditions as before. The ring still breaks up, but solution converges to a lattice-like relative equilibrium, rather than chaos. The dashed circle is the asymptotic prediction, see our preprint.
Damped dynamics (3) leading to stable lattice