Abstract Harmonic AnalysisThe class of locally compact groups is large enough to encompass many/most of the topological groups that arise in physics, geometry, number theory and other areas of mathematics and the natural sciences. Moreover, any abstract group is a topological group when endowed with the discrete toplogy. In all these examples of interesting groups, the representations of the groups have meaningful interpretations and applications. I am particularly interested in the dual spaces of locally compact groups and the influence that the topological properties of the dual space have on the analysis of functions on the group. If G is a locally compact group, the set of equivalence classes of irreducible unitary representations of G is denoted G^ and is called the dual space of G. There is a natural topology on G^ which usually fails to be Hausdorff. It is the non-Hausdorff character of most dual spaces that leads to much of the fun. | |
By clicking on the image below, you will (hopefully) see a big drawing of one
of my favorite dual spaces. The group whose dual is pictured below
is the fundamental
group of the Klein bottle. It happens to also be one of the 17 two
dimensional crystal groups and in that collection carries the name pg,
so that is what I will call it here.
| |
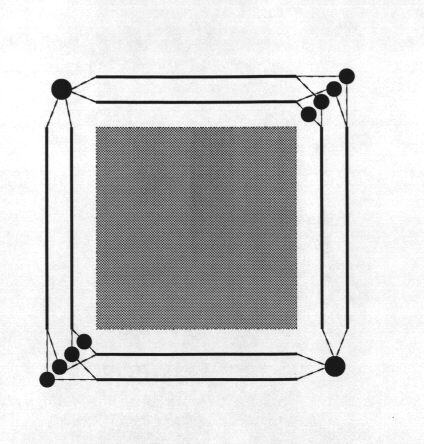
Another two dimensional crystal group that has an interesting dual is
pgg. A picture of pgg^ is shown below. I will leave it to you to
try and sort out how the non-Hausdorff nature of the topology is being
represented. The central square is an open square of 4-dimensional
representations. The
interesting pattern in the central square is just a jpeg artifact that means
nothing. The points on the horizontal and vertical solid lines each
represent 2-dimensional representations. The upper left and lower right
big dots are each 2-dimensional representations and all the other dots are
1-dimensional.
|
Last modified, July 8, 2004