Derivatives in Curve Sketching

Derivatives can help graph many functions. The first derivative of a function is the slope of the tangent line for any point on the function! Therefore, it tells when the function is increasing, decreasing or where it has a horizontal tangent! Consider the following graph:

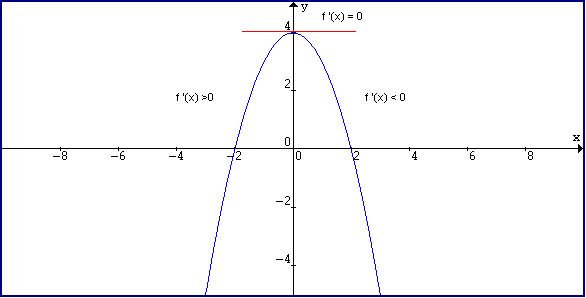
Notice on the left side, the function is increasing and the slope of the tangent line is positive. At the vertex point of the parabola, the tangent is a horizontal line, meaning f '(x) = 0 and on the right side the graph is decreasing and the slope of the tangent line is negative!

These observations lead to a generalization for any function f(x) that has a derivative on an interval I :

• 1) If f '(x) > 0 on an interval I, then the graph of f(x) rises as x increases.
• 2) If f '(x) < 0 on an interval I, then the graph of f(x) falls as x increases.
• 3) If f '(c) = 0, then the graph of f(x) has a horizontal tangent at x = c. The function may have a local maximum or minimum value, or a point of inflection.

Here are some graphs of each of the observations made above!

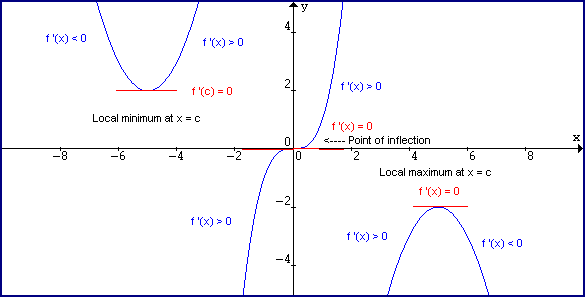
Some observations on the above graphs!

1) To be a minimum point, the graph must change direction from decreasing to increasing.

2) To be a maximum point, the graph must change direction from increasing to decreasing.

3) To be an inflection point, the graph doesn't change direction. In the above example ( one in middle) it is increasing before the f '(c) = 0 and it is still increasing after. You can also have one with the graph decreasing on both sides.

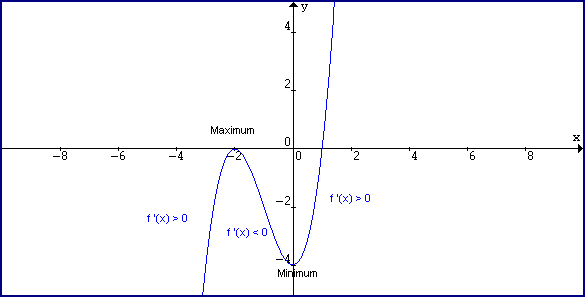
1)  Find the critical points(maximum, minimum or inflection points) of the function f(x) = x³ + 3x² - 4. Then graph the function.
a)  Find the critical points by finding f '(x).

Find the zeros by solving f '(x) = 0
3x² + 6x = 0 3x(x + 2) = 0
Therefore, we have critical points at x = 0, and x = -2

Substitute these values into the original function to find the y values of the critical points. The points are (0, -4) and (-2, 0)

b)  Use the derivative to find where the graph is increasing and decreasing by taking x values in each of the three areas formed by the two critical points.  The chart below shows the results
 

	f '(x)
x < -2	+
x = -2	0
-2 < x < 0	-
x = 0	0
x > 0	+

 

The chart shows that (-2, 0) is a local Max. and (0, -4) is a local min.  You can tell because of the sign changes!

c)  Find the zeros of the original function.  These are the x-intercepts.  You can use synthetic division and factoring to find the zeros!  They are (-2, 0) (double root) and (1, 0)

d)  Find the y-intercept.  This is the constant of the original function.  (0, -4)

e)  Now take the limit as x goes to both infinities of the original function.   

f)  Now put all these together and graph the function!



 

2) Find the critical points and graph f(x) = x⁴ - 8x² + 9
a) Find the critical points by finding f '(x)
f '(x) = 4x³ - 16x
Set f '(x) = 0 and solve
4x³ - 16x = 0
4x(x² - 4) = 0
4x(x - 2)(x + 2) = 0
Therefore, the critical points are at x = 0, x = 2 and x = -2
Substitute these into the original function and the points are (0, 9), (2, -7), (-2, -7)
b) Use the derivative to find the slope in each of the four areas divided by the three critical points. The chart is below

	f '(x)
x < -2	-
x = -2	0
-2 < x < 0	+
x = 0	0
0 < x < 2	-
x = 2	0
x > 2

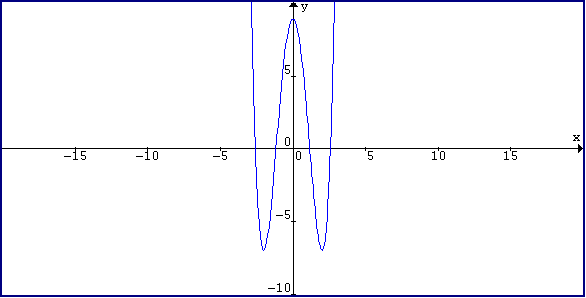
The chart shows that (-2, -7) and (2, 7) are minimums and (0, 9) is a maximum. Check out the signs on the chart to realize this!
c) Find the zeros of the original function by using your graphing calculator. The zeros are not rational but irrational.

d) The y intercept is (0, 9) e) Find the limits on infinity.

f) Put these together and graph the function!

1) What are the x-intercepts of f(x)?
(1, 0)
(-2, 0)
(0, 0)
(1, 0) and (-2, 0)
doesn't cross x axis

2) What are the critical points?
(-2, 0) and (0, 0)
(-2, 0) and (0, -4)
(1, 0) and (0, 0)
(1, 0) and (0, -4)
Just (0, 0)

3) Which point is a local maximum?
(-2, 0)
(0, 0)
(1, 0)
(0, -4)
doesn't have one

3) What point is a local minimum?
(-2, 0)
(0, 0)
(1, 0)
(0, -4)
doesn't have one

3) What point is an inflection point(critical)?
(-2, 0)
(0, 0)
(1, 0)
(0, -4)
doesn't have one