bl.mws

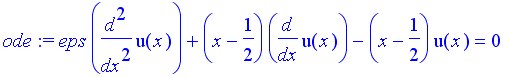
>    restart;

>    # Set up the ODE and boundary conditions:
ode := eps*diff(u(x),x,x)+(x-1/2)*diff(u(x),x)-(x-1/2)*u(x)=0;
bc := {u(0)=-2, u(1)=exp(1.)};

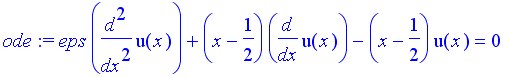
ode := eps*diff(u(x),`$`(x,2))+(x-1/2)*diff(u(x),x)-(x-1/2)*u(x) = 0

bc := {u(0) = -2, u(1) = 2.718281828}

>    # The uniform asymptotic expansion is given by:
unif := exp(x)*(-1/2+3/2*sqrt(2/Pi)*
int(exp(-s^2/2), s=0..(x-1/2)/eps^(1/2)));

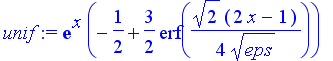
unif := exp(x)*(-1/2+3/2*erf(1/4*2^(1/2)*(2*x-1)/eps^(1/2)))

>    eps := 0.01;

eps := .1e-1

>    # Solve the problem numerically:
pp := dsolve({ode} union bc, numeric);

pp := proc (x_bvp) local res, data, solnproc, ndsol, outpoint, i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 14; if _EnvInFsol...

>    # Plot the solution and compare with the asymptotic expansion:
with(plots):

>    odeplot(pp, [[x, u(x)], [x, unif]]);

[Maple Plot]

>    # Save this plot for future use:
pic := %:

>   

>    # Try another epsilon value:

>    eps := 0.001;

eps := .1e-2

>    pp := dsolve({ode} union bc, numeric);

pp := proc (x_bvp) local res, data, solnproc, ndsol, outpoint, i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 14; if _EnvInFsol...

>    odeplot(pp, [[x, u(x)], [x, unif]]);

[Maple Plot]

>    display(%, pic);

[Maple Plot]

>   

>