DISP Mathematics (Scie 1500R)

MAPLE Lab. Tutorial 6 Differential equations & Integration Monday February 21.



1 DIFFERENTIAL EQUATIONS.

MAPLE can solve many of the differential equations that one finds in Calculus books. The basic command is dsolve. This requires two arguments, the first should be the differential equation you want to solve, and the second the variable you want to solve for. There are a variety of extra options that we won't go into here. However, if the differential equation has initial conditions, then these extra equations go together with the first argument (the differential equation) and one puts everything together as a set of equations inside curly brackets $\{\ldots\}$.

Example. To solve the differential equation (this is # 5 from §6.5 of E & P).

\begin{displaymath}\frac{dy}{dx} = 2x\sqrt{y-1}\end{displaymath}

We type the following:
> deq:= diff(y(x),x) = 2*x*sqrt(y-1);
> dsolve(deq,y(x));
Note that in both lines one needs to say that $y$ dependson $x$ by typing y(x). Note, also, that unlike indefinite integration, here MAPLE does give you an arbitrary constant C_1.

If, now, you want to get $y(x)$ explicitly as a function of $x$ then you can try:
> y(x) = solve(%,y(x));

For initial conditions the commands are as follows.
§6.5 # 15 (you have # 14 for the assignment) Solve the differential equation:

\begin{displaymath}\frac{dy}{dx} = \sqrt{xy^3}, \quad y(0) = 4.\end{displaymath}

> deq2:= diff(y(x),x) =x$\,^{\wedge}$(1/2)*y$\,^{\wedge}$(3/2);
dsolve({deq2, y(0) = 4},y(x));
One needs to be a bit careful using dsolve. For instance, it is surprising that if one types the above equation as
> deq3:=diff(y(x),x) = sqrt(x*y$\,^{\wedge}$3);
and then uses
> dsolve(deq3,y(x));
one gets a horrendous expression! And, because of this, MAPLE is unable to solve the equation in this form with the initial condition.

2 INTEGRATION

Just to remind you from last week, the command for indefinite integration is
> int(f(x), x);
but this does NOT give you an arbitrary constant at the end (you must supply that). For definite integration, the command is
> int(f(x), x=a..b);
Note that in both of these, $f(x)$ is an expression.
MAPLE will try and do the definite integral symbolically and give an exact answer. If it cannot do so, it will return the expression for the integral. To evaluate integrals exactly, use > value(.); to get a decimal approximation use > evalf(.);

3 EXERCISES

NAME STUDENT #

Before you start these exercises type
> restart;

You are now in a position to use MAPLE to do your assignments if you wish. If you do so, please indicate that that is what you have done, and give your MAPLE command, by writing
``MAPLE command: > ''
followed by ``To which MAPLE gives ''

I don't have a lot of time to cover all the methods of integration in Chapter 9. However, MAPLE knows how to do most of them. To illustrate this the tutorial this week is to do a sample of integrals from various sections of Chapter 9 that we have not covered.

Use MAPLE to evaluate the following integrals. After getting an answer, CHECK it by differentiation ( > diff(%,x); and, if necessary, > simplify(%); or > simplify(%,trig);).

1. # 9 p.517 $\int (1+\sin x)^5 \cos x \,dx.$

2. # 17 p.524 $\int x^5\sqrt{x^3 + 1}\,dx.$

3. # 35 p.524 $\int x^3 \sin(x^2) \,dx.$

4. The book states the following: ``An advertisement for a symbolic algebra program claims that an engineer worked for three weeks on the following integral and never got the same answer twice''. May be the ad was for MAPLE.

# 63 p.525 $\int (k\ln x -2x^3 +3x^2 +b) \,dx$. DON'T write out the solution!!! Instead evaluate (to 4 decimal places) the definite integral from 1 to 2 when $k =2$ and $b=1$.

5. # 11 p.532 $\int (\sin(x))^3 \,dx.$

6. # 13 p.532 $\int (\sin(x))^2 (\cos(x))^3 \,dx.$

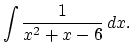
7. # 5 p.540 $ \displaystyle \int\frac{1}{x^2 +x - 6} \,dx.$

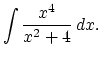
8. # 9 p.540 $\displaystyle \int\frac{x^4}{x^2 +4} \,dx.$

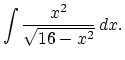
9. #5 p.547 $\displaystyle \int\frac{x^2}{\sqrt{16-x^2}} \,dx.$

10. #11 p.547 $\int x^3 \sqrt{9+4x^2} \,dx.$


Tony Thompson
2000-08-28