Selinger's normal form for symplectic group Sp(2n, Zp)

This program implements an algorithm that is similar to the one in Proposition 5.5 in the paper Generators and relations for n-qubit Clifford operators. It normalizes any element of Sp(2n, p) to a normal form that is similar to the one in Definition 4.3. We use the generating set {S, H, CZ, Ex}, and their action on Zp^(2n) is:

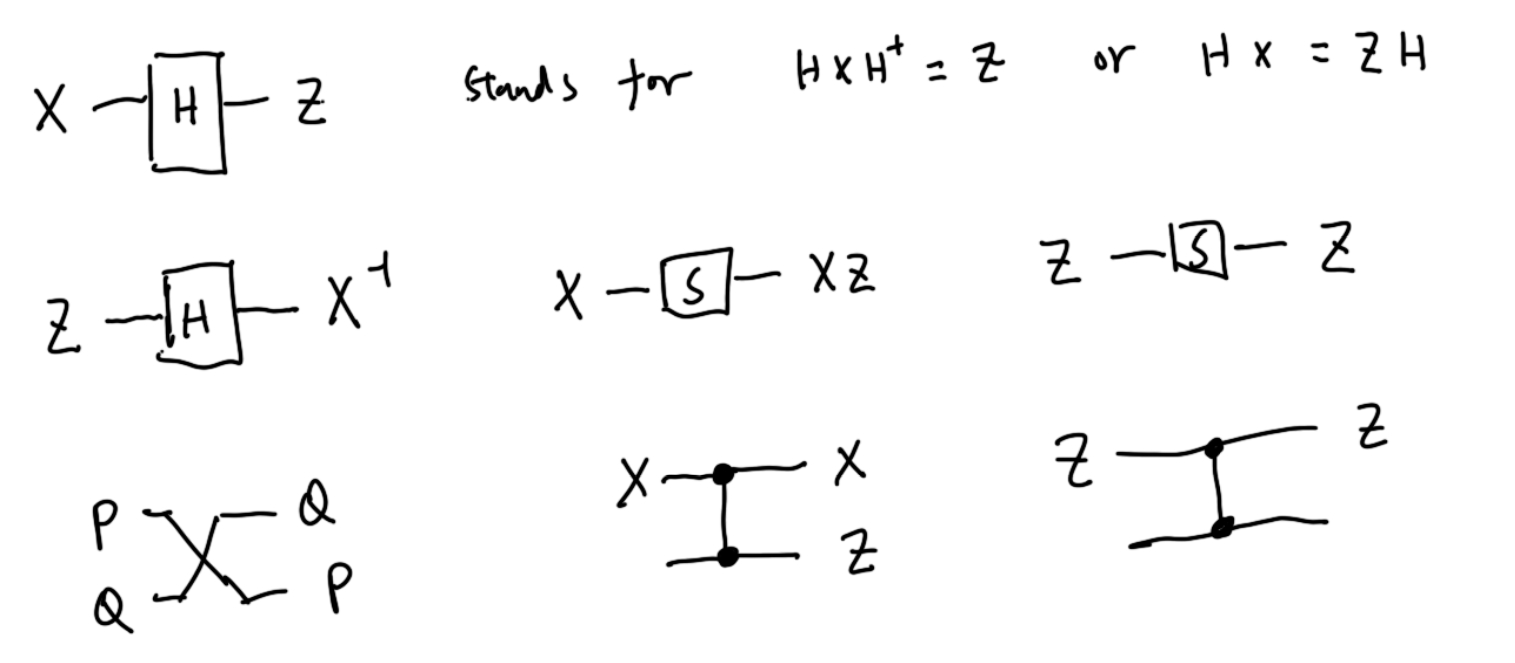
We support upto 11 pits (wires). Here is an example; the left-handside normalizes to a stair-like normal form on the right.

We will disclose the definition of A, B, D, E boxes later. They have similar structures as in Selinger's paper and in paper A Complete and Natural Rule Set for Multi-Qutrit Clifford Circuits .

Step 1. Input a pair of a prime and a circuit consisting of gates {S, H, CZ, Ex, M}.

S 0 is S on the first qupit (counting from 0, top to bottom). Ex j is Swap gate on j-th and (j+1)-th qupit. CZ j k is controlled Z gate on qupit j and k. M j e is the multiplier on j-th qupit sending X = (1,0) in Zp ^ 2 to X ^ e = (e, 0). NOTE: e must not be 0 mod your prime. Gate sequence is parsed in circuit mode, i.e. SH is S;H or H*S, where * is matrix multiplication. For example,

(5,[S 1,H 2,CZ 0 1,Ex 3])

Step 2. Click Normalize button

See Also

Finding MA normal forms for single qubit operators.

Opened on: 08/30/2025. Last edited on: 08/30/2025