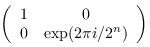| Safe Haskell | None |
|---|
Quipper
Contents
Description
This is the main export module for Quipper, collecting everything that Quipper applications need. This is Quipper's "public" interface.
Synopsis
- data Circ a
- data Qubit
- data Bit
- type Qulist = [Qubit]
- type Bitlist = [Bit]
- type Timestep = Double
- qnot :: Qubit -> Circ Qubit
- hadamard :: Qubit -> Circ Qubit
- gate_H :: Qubit -> Circ Qubit
- gate_X :: Qubit -> Circ Qubit
- gate_Y :: Qubit -> Circ Qubit
- gate_Z :: Qubit -> Circ Qubit
- gate_S :: Qubit -> Circ Qubit
- gate_S_inv :: Qubit -> Circ Qubit
- gate_T :: Qubit -> Circ Qubit
- gate_T_inv :: Qubit -> Circ Qubit
- gate_E :: Qubit -> Circ Qubit
- gate_E_inv :: Qubit -> Circ Qubit
- gate_omega :: Qubit -> Circ Qubit
- gate_V :: Qubit -> Circ Qubit
- gate_V_inv :: Qubit -> Circ Qubit
- expZt :: Timestep -> Qubit -> Circ Qubit
- rGate :: Int -> Qubit -> Circ Qubit
- gate_W :: Qubit -> Qubit -> Circ (Qubit, Qubit)
- gate_iX :: Qubit -> Circ Qubit
- gate_iX_inv :: Qubit -> Circ Qubit
- global_phase :: Double -> Circ ()
- global_phase_anchored :: QCData qc => Double -> qc -> Circ ()
- qmultinot :: QData qa => qa -> Circ qa
- cnot :: Bit -> Circ Bit
- swap :: QCData qc => qc -> qc -> Circ (qc, qc)
- qnot_at :: Qubit -> Circ ()
- hadamard_at :: Qubit -> Circ ()
- gate_H_at :: Qubit -> Circ ()
- gate_X_at :: Qubit -> Circ ()
- gate_Y_at :: Qubit -> Circ ()
- gate_Z_at :: Qubit -> Circ ()
- gate_S_at :: Qubit -> Circ ()
- gate_S_inv_at :: Qubit -> Circ ()
- gate_T_at :: Qubit -> Circ ()
- gate_T_inv_at :: Qubit -> Circ ()
- gate_E_at :: Qubit -> Circ ()
- gate_E_inv_at :: Qubit -> Circ ()
- gate_omega_at :: Qubit -> Circ ()
- gate_V_at :: Qubit -> Circ ()
- gate_V_inv_at :: Qubit -> Circ ()
- expZt_at :: Timestep -> Qubit -> Circ ()
- rGate_at :: Int -> Qubit -> Circ ()
- gate_W_at :: Qubit -> Qubit -> Circ ()
- gate_iX_at :: Qubit -> Circ ()
- gate_iX_inv_at :: Qubit -> Circ ()
- qmultinot_at :: QData qa => qa -> Circ ()
- cnot_at :: Bit -> Circ ()
- swap_at :: QCData qc => qc -> qc -> Circ ()
- qinit :: QShape ba qa ca => ba -> Circ qa
- qterm :: QShape ba qa ca => ba -> qa -> Circ ()
- qdiscard :: QData qa => qa -> Circ ()
- cinit :: QShape ba qa ca => ba -> Circ ca
- cterm :: QShape ba qa ca => ba -> ca -> Circ ()
- cdiscard :: CData ca => ca -> Circ ()
- qc_init :: QCData qc => BType qc -> Circ qc
- qc_init_with_shape :: QCData qc => qc -> BType qc -> Circ qc
- qc_term :: QCData qc => BType qc -> qc -> Circ ()
- qc_discard :: QCData qc => qc -> Circ ()
- measure :: QShape ba qa ca => qa -> Circ ca
- prepare :: QShape ba qa ca => ca -> Circ qa
- qc_measure :: QCData qc => qc -> Circ (QCType Bit Bit qc)
- qc_prepare :: QCData qc => qc -> Circ (QCType Qubit Qubit qc)
- cgate_xor :: [Bit] -> Circ Bit
- cgate_eq :: Bit -> Bit -> Circ Bit
- cgate_not :: Bit -> Circ Bit
- cgate_and :: [Bit] -> Circ Bit
- cgate_or :: [Bit] -> Circ Bit
- cgate_if :: CData ca => Bit -> ca -> ca -> Circ ca
- circ_if :: CData ca => Bit -> Circ ca -> Circ ca -> Circ ca
- named_gate :: QData qa => String -> qa -> Circ qa
- named_gate_at :: QData qa => String -> qa -> Circ ()
- named_rotation :: QData qa => String -> Timestep -> qa -> Circ qa
- named_rotation_at :: QData qa => String -> Timestep -> qa -> Circ ()
- extended_named_gate :: (QData qa, QData qb) => String -> qa -> qb -> Circ qa
- extended_named_gate_at :: (QData qa, QData qb) => String -> qa -> qb -> Circ ()
- dynamic_lift :: QShape ba qa ca => ca -> Circ ba
- qinit_plusminus :: Bool -> Circ Qubit
- qinit_of_char :: Char -> Circ Qubit
- qinit_of_string :: String -> Circ [Qubit]
- map_hadamard :: QData qa => qa -> Circ qa
- map_hadamard_at :: QData qa => qa -> Circ ()
- controlled_not :: QCData qc => qc -> qc -> Circ (qc, qc)
- controlled_not_at :: QCData qc => qc -> qc -> Circ ()
- bool_controlled_not :: QCData qc => qc -> BType qc -> Circ qc
- bool_controlled_not_at :: QCData qc => qc -> BType qc -> Circ ()
- qc_copy :: QCData qc => qc -> Circ qc
- qc_uncopy :: QCData qc => qc -> qc -> Circ ()
- qc_copy_fun :: QCData qc => qc -> Circ (qc, qc)
- qc_uncopy_fun :: QCData qc => qc -> qc -> Circ qc
- mapUnary :: QData qa => (Qubit -> Circ Qubit) -> qa -> Circ qa
- mapBinary :: QData qa => (Qubit -> Qubit -> Circ (Qubit, Qubit)) -> qa -> qa -> Circ (qa, qa)
- mapBinary_c :: QShape ba qa ca => (Qubit -> Bit -> Circ (Qubit, Bit)) -> qa -> ca -> Circ (qa, ca)
- qc_mapBinary :: QCData qc => (Qubit -> Qubit -> Circ (Qubit, Qubit)) -> (Bit -> Bit -> Circ (Bit, Bit)) -> qc -> qc -> Circ (qc, qc)
- class ControlSource a where
- to_control :: a -> ControlList
- data ControlList
- (.&&.) :: (ControlSource a, ControlSource b) => a -> b -> ControlList
- (.==.) :: QCData qc => qc -> BType qc -> ControlList
- (./=.) :: QCLeaf q => q -> Bool -> ControlList
- controlled :: ControlSource c => Circ a -> c -> Circ a
- data Signed a = Signed a Bool
- from_signed :: Signed a -> a
- get_sign :: Signed a -> Bool
- comment :: String -> Circ ()
- label :: Labelable qa labels => qa -> labels -> Circ ()
- comment_with_label :: Labelable qa labels => String -> qa -> labels -> Circ ()
- without_comments :: Circ a -> Circ a
- class Labelable a s
- box :: (QCData qa, QCData qb, QCurry qa_qb qa qb) => String -> qa_qb -> qa_qb
- nbox :: QCData qa => String -> Integer -> (qa -> Circ qa) -> qa -> Circ qa
- box_loopM :: (Integral int, QCData qa) => String -> int -> qa -> (qa -> Circ qa) -> Circ qa
- loopM_boxed_if :: (Integral int, QCData qa) => Bool -> String -> int -> qa -> (qa -> Circ qa) -> Circ qa
- with_ancilla :: (Qubit -> Circ a) -> Circ a
- with_ancilla_list :: Int -> (Qulist -> Circ a) -> Circ a
- with_ancilla_init :: QShape a qa ca => a -> (qa -> Circ b) -> Circ b
- with_computed_fun :: (QCData x, QCData y) => x -> (x -> Circ y) -> (y -> Circ (y, b)) -> Circ (x, b)
- with_computed :: QCData x => Circ x -> (x -> Circ b) -> Circ b
- with_basis_change :: Circ () -> Circ b -> Circ b
- with_controls :: ControlSource c => c -> Circ a -> Circ a
- with_classical_control :: QCData qa => Bit -> String -> qa -> (qa -> Circ qa) -> Circ qa
- without_controls :: Circ a -> Circ a
- without_controls_if :: NoControlFlag -> Circ a -> Circ a
- for :: Monad m => Int -> Int -> Int -> (Int -> m ()) -> m ()
- endfor :: Monad m => m ()
- foreach :: Monad m => [a] -> (a -> m b) -> m ()
- loop :: (Eq int, Num int) => int -> t -> (t -> t) -> t
- loop_with_index :: (Eq int, Num int) => int -> t -> (int -> t -> t) -> t
- loopM :: (Eq int, Num int, Monad m) => int -> t -> (t -> m t) -> m t
- loop_with_indexM :: (Eq int, Num int, Monad m) => int -> t -> (int -> t -> m t) -> m t
- reverse_generic :: (QCData x, QCData y, TupleOrUnary xt x, QCurry x_y x y, Curry x_y_xt x (y -> Circ xt)) => x_y -> x_y_xt
- reverse_simple :: (QCData_Simple x, QCData y, TupleOrUnary xt x, QCurry x_y x y) => x_y -> y -> Circ xt
- reverse_generic_endo :: (QCData x, TupleOrUnary xt x, QCurry x_xt x xt) => x_xt -> x_xt
- reverse_generic_imp :: (QCData x, QCurry x__ x ()) => x__ -> x__
- reverse_generic_curried :: (QCData x, QCData y, TupleOrUnary xt x, Tuple yt y, QCurry x_yt x yt, QCurry y_xt y xt, Curry x_y_xt x y_xt) => x_yt -> x_y_xt
- reverse_simple_curried :: (QCData_Simple x, QCData y, TupleOrUnary xt x, Tuple yt y, QCurry x_yt x yt, QCurry y_xt y xt) => x_yt -> y_xt
- reverse_endo_if :: (QCData x, TupleOrUnary xt x, QCurry x_xt x xt) => Bool -> x_xt -> x_xt
- reverse_imp_if :: (QCData qa, QCurry fun qa ()) => Bool -> fun -> fun
- data Format
- = EPS
- | PS
- | ASCII
- | Preview
- | GateCount
- | CustomStyle FormatStyle
- data FormatStyle = FormatStyle {
- renderformat :: RenderFormat
- backgroundcolor :: Color
- foregroundcolor :: Color
- linewidth :: Double
- coffs :: Double
- dotradius :: Double
- oplusradius :: Double
- xoff :: Double
- gatepad :: Double
- gateheight :: Double
- crossradius :: Double
- stringbase :: Double
- barwidth :: Double
- barheight :: Double
- dwidth :: Double
- dheight :: Double
- maxgatelabelwidth :: Double
- maxlabelwidth :: Double
- maxnumberwidth :: Double
- gatefont :: Font
- commentfont :: Font
- commentcolor :: Color
- labelfont :: Font
- labelcolor :: Color
- numberfont :: Font
- numbercolor :: Color
- subroutineshape :: Bool
- format_enum :: [(String, Format)]
- print_unary :: QCData qa => Format -> (qa -> Circ b) -> qa -> IO ()
- print_generic :: (QCData qa, QCurry qfun qa b, Curry fun qa (IO ())) => Format -> qfun -> fun
- print_simple :: (QCData qa, QCurry qfun qa b, Curry fun qa (IO ()), QCData_Simple qa) => Format -> qfun -> IO ()
- print_of_document :: Format -> Document a -> IO a
- print_of_document_custom :: Custom -> Format -> Document a -> IO a
- classical_to_cnot :: (QCData qa, QCData qb, QCurry qfun qa qb) => qfun -> qfun
- classical_to_quantum :: (QCData qa, QCData qb, QCurry qfun qa qb, QCurry qfun' (QType qa) (QType qb)) => qfun -> qfun'
- classical_to_reversible :: (QCData qa, QCData qb) => (qa -> Circ qb) -> (qa, qb) -> Circ (qa, qb)
- type Transformer m a b = forall x. T_Gate m a b x -> x
- data T_Gate m a b x
- = T_QGate String Int Int InverseFlag NoControlFlag (([a] -> [a] -> Ctrls a b -> m ([a], [a], Ctrls a b)) -> x)
- | T_QRot String Int Int InverseFlag Timestep NoControlFlag (([a] -> [a] -> Ctrls a b -> m ([a], [a], Ctrls a b)) -> x)
- | T_GPhase Double NoControlFlag (([B_Endpoint a b] -> Ctrls a b -> m (Ctrls a b)) -> x)
- | T_CNot NoControlFlag ((b -> Ctrls a b -> m (b, Ctrls a b)) -> x)
- | T_CGate String NoControlFlag (([b] -> m (b, [b])) -> x)
- | T_CGateInv String NoControlFlag ((b -> [b] -> m [b]) -> x)
- | T_CSwap NoControlFlag ((b -> b -> Ctrls a b -> m (b, b, Ctrls a b)) -> x)
- | T_QPrep NoControlFlag ((b -> m a) -> x)
- | T_QUnprep NoControlFlag ((a -> m b) -> x)
- | T_QInit Bool NoControlFlag (m a -> x)
- | T_CInit Bool NoControlFlag (m b -> x)
- | T_QTerm Bool NoControlFlag ((a -> m ()) -> x)
- | T_CTerm Bool NoControlFlag ((b -> m ()) -> x)
- | T_QMeas ((a -> m b) -> x)
- | T_QDiscard ((a -> m ()) -> x)
- | T_CDiscard ((b -> m ()) -> x)
- | T_DTerm Bool ((b -> m ()) -> x)
- | T_Subroutine BoxId InverseFlag NoControlFlag ControllableFlag [Wire] Arity [Wire] Arity RepeatFlag ((Namespace -> [B_Endpoint a b] -> Ctrls a b -> m ([B_Endpoint a b], Ctrls a b)) -> x)
- | T_Comment String InverseFlag (([(B_Endpoint a b, String)] -> m ()) -> x)
- identity_transformer :: Transformer Circ Qubit Bit
- transform_generic :: (QCData x, QCData y, QCurry qfun x y) => Transformer Circ Qubit Bit -> qfun -> qfun
- transform_generic_shape :: (QCData x, QCData y, QCurry qfun x y, Curry qfun' x' (m y'), Curry qfun'' x qfun', x' ~ QCType a b x, y' ~ QCType a b y, Monad m) => Transformer m a b -> qfun -> qfun''
- type InverseFlag = Bool
- type NoControlFlag = Bool
- data B_Endpoint a b
- = Endpoint_Qubit a
- | Endpoint_Bit b
- type Endpoint = B_Endpoint Qubit Bit
- type Ctrls a b = [Signed (B_Endpoint a b)]
- module Quipper.Internal.CircLifting
- module Quipper.Utils.Template
- type QShape ba qa ca = (QData qa, BType qa ~ ba, CType qa ~ ca)
- type QData qa = (qa ~ QType (CType qa), qa ~ QTypeB (BType qa), qa ~ QCType Qubit Bool qa, qa ~ QType qa, QCData qa, QCData (CType qa))
- type CData ca = (QData (QType ca), CType (QType ca) ~ ca)
- type BData ba = (QData (QTypeB ba), BType (QTypeB ba) ~ ba)
- class (Labelable qc String, Typeable qc, Show qc, Show (LType qc), qc ~ QCType Qubit Bit qc, CType (QType qc) ~ CType qc, BType (CType qc) ~ BType qc, QCType Int Bool (CType qc) ~ BType qc) => QCData qc
- type QCDataPlus qc = (QCData qc, QData (QType qc))
- bit :: Bit
- qubit :: Qubit
- qshape :: QData qa => BType qa -> qa
- qc_false :: QCData qc => qc -> BType qc
- type QEq qc = QCData qc
- q_is_equal :: QEq qc => qc -> qc -> Circ (qc, qc, Qubit)
- q_is_not_equal :: QEq qc => qc -> qc -> Circ (qc, qc, Qubit)
- class (QEq qa, QData qa) => QOrd qa where
- q_lt :: QOrd qa => qa -> qa -> Circ (qa, qa, Qubit)
- q_gt :: QOrd qa => qa -> qa -> Circ (qa, qa, Qubit)
- q_le :: QOrd qa => qa -> qa -> Circ (qa, qa, Qubit)
- q_ge :: QOrd qa => qa -> qa -> Circ (qa, qa, Qubit)
The Circ monad
The Circ monad encapsulates the type of quantum operations. For
example, a quantum operation that inputs two Qubits and outputs a
Qubit and a Bit has the following type:
(Qubit, Qubit) -> Circ (Qubit, Bit)
Instances
| Monad Circ # | |
| Functor Circ # | |
| MonadFail Circ # | |
Defined in Quipper.Internal.Monad | |
| Applicative Circ # | |
| QCurry (Circ b) () b # | |
| CircLiftingUnpack (Circ [a]) (Circ [a]) # | |
| CircLiftingUnpack (Circ ()) (Circ ()) # | |
| CircLiftingUnpack (Circ (a, b)) (Circ (a, b)) # | |
| CircLiftingUnpack (Circ (a, b, c)) (Circ (a, b, c)) # | |
| CircLiftingUnpack (Circ (a, b, c, d)) (Circ (a, b, c, d)) # | |
| CircLiftingUnpack (Circ (a, b, c, d, e)) (Circ (a, b, c, d, e)) # | |
| CircLiftingUnpack (Circ (a, b, c, d, e, f)) (Circ (a, b, c, d, e, f)) # | |
| CircLiftingUnpack (Circ (a, b, c, d, e, f, g)) (Circ (a, b, c, d, e, f, g)) # | |
| CircLiftingUnpack (Circ Qubit) (Circ Qubit) # | |
| CircLiftingUnpack (Circ b) b' => CircLiftingUnpack (Circ (a -> Circ b)) (a -> b') # | |
Basic types
The type of qubits.
Instances
| Eq Qubit # | |
| Ord Qubit # | |
| Show Qubit # | |
| ControlSource Qubit # | |
Defined in Quipper.Internal.Monad Methods to_control :: Qubit -> ControlList Source # | |
| QCLeaf Qubit # | |
Defined in Quipper.Internal.QData | |
| SimpleType Qubit # | |
Defined in Quipper.Internal.QData | |
| QCData Qubit # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Qubit -> (q -> m q') -> (c -> m c') -> QCType q c Qubit -> m (QCType q' c' Qubit) Source # qcdata_zip :: Qubit -> q -> c -> q' -> c' -> QCType q c Qubit -> QCType q' c' Qubit -> ErrMsg -> QCType (q, q') (c, c') Qubit Source # qcdata_promote :: BType Qubit -> Qubit -> ErrMsg -> BType Qubit Source # | |
| Labelable Qubit String # | |
Defined in Quipper.Internal.Labels | |
| ControlSource (Signed Qubit) # | |
Defined in Quipper.Internal.Monad Methods to_control :: Signed Qubit -> ControlList Source # | |
| CircLiftingUnpack (Circ Qubit) (Circ Qubit) # | |
| type QCType x y Qubit # | |
Defined in Quipper.Internal.QData | |
The type of run-time classical bits (i.e., boolean wires in a circuit).
Instances
| Eq Bit # | |
| Ord Bit # | |
| Show Bit # | |
| ControlSource Bit # | |
Defined in Quipper.Internal.Monad Methods to_control :: Bit -> ControlList Source # | |
| QCLeaf Bit # | |
Defined in Quipper.Internal.QData | |
| SimpleType Bit # | |
Defined in Quipper.Internal.QData | |
| QCData Bit # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Bit -> (q -> m q') -> (c -> m c') -> QCType q c Bit -> m (QCType q' c' Bit) Source # qcdata_zip :: Bit -> q -> c -> q' -> c' -> QCType q c Bit -> QCType q' c' Bit -> ErrMsg -> QCType (q, q') (c, c') Bit Source # qcdata_promote :: BType Bit -> Bit -> ErrMsg -> BType Bit Source # | |
| Labelable Bit String # | |
Defined in Quipper.Internal.Labels | |
| ControlSource (Signed Bit) # | |
Defined in Quipper.Internal.Monad Methods to_control :: Signed Bit -> ControlList Source # | |
| type QCType x y Bit # | |
Defined in Quipper.Internal.QData | |
Basic gates
This section contains various elementary gates that can be used as building blocks for constructing circuits.
type Timestep = Double Source #
A time step is a small floating point number used as a parameter to certain gates, such as rotation gates or the e−iZt gate.
Reversible gates in functional style
The gates in this section are in "functional" style, which means
that they return something. For example, the qnot gate consumes a
Qubit, performs an operation, and outputs a new Qubit. The
gates should be used like this:
output <- qnot input
or, for a binary gate:
(out0, out1) <- gate_W in0 in1
For each of these gates, we also provide a version in imperative style, see Reversible gates in imperative style below.
gate_E :: Qubit -> Circ Qubit Source #
Apply a Clifford E = HS3ω3 gate.
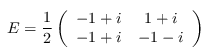
This gate is the unique Clifford operator with the properties E³ = I, EXE⁻¹ = Y, EYE⁻¹ = Z, and EZE⁻¹ = X. It is a convenient gate for calculations. For example, every Clifford operator can be uniquely written of the form
- EaXbScωd,
where a, b, c, and d are taken modulo 3, 2, 4, and 8, respectively.
gate_V :: Qubit -> Circ Qubit Source #
Apply a V = √X gate. This is by definition the following gate (see also Nielsen and Chuang, p.182):
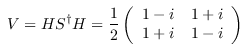
expZt :: Timestep -> Qubit -> Circ Qubit Source #
Apply an e−iZt gate. The timestep t is a parameter.
gate_W :: Qubit -> Qubit -> Circ (Qubit, Qubit) Source #
Apply a W gate. The W gate is self-inverse and diagonalizes the SWAP gate.
The arguments are such that
gate_W |0〉 |0〉 = |00〉 gate_W |0〉 |1〉 = (|01〉+|10〉) / √2 gate_W |1〉 |0〉 = (|01〉-|10〉) / √2 gate_W |1〉 |1〉 = |11〉.
In circuit diagrams, W1 denotes the "left" qubit, and W2 denotes the "right" qubit.
gate_iX :: Qubit -> Circ Qubit Source #
Apply an iX gate. This gate is used similarly to the Pauli X gate, but with two advantages:
- the doubly-controlled iX gate can be implemented in the Clifford+T gate base with T-count 4 (the doubly-controlled X gate requires T-count 7);
- the iX-gate has determinant 1, and therefore an n-times controlled iX gate can be implemented in the Clifford+T gate base with no ancillas.
In particular, the iX gate can be used to implement an additional control with T-count 8, like this:
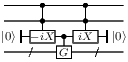
global_phase :: Double -> Circ () Source #
Apply a global phase change eiπt, where typically t ∈ [0,2]. This gate is uninteresting if not controlled; however, it has non-trivial effect if it is used as a controlled gate.
global_phase_anchored :: QCData qc => Double -> qc -> Circ () Source #
Like global_phase, except the gate is also "anchored" at a
qubit, a bit, or more generally at some quantum data. The anchor
is only used as a hint for graphical display. The gate, which is a
zero-qubit gate, will potentially be displayed near the anchor(s).
swap :: QCData qc => qc -> qc -> Circ (qc, qc) Source #
Apply a swap gate to two qubits. More generally, apply swap gates to every corresponding pair of qubits in two pieces of quantum data.
Reversible gates in imperative style
The gates in this section are in "imperative" style, which means that they operate on a qubit "in place" and do not return anything. The gates should be used like this:
qnot_at q
or, for a binary gate:
gate_W_at q0 q1
For each of these gates, we also provide a version in functional style, see Reversible gates in functional style above.
hadamard_at :: Qubit -> Circ () Source #
Apply a Hadamard gate.
gate_S_inv_at :: Qubit -> Circ () Source #
Apply the inverse of an S-gate.
gate_T_inv_at :: Qubit -> Circ () Source #
Apply the inverse of a T-gate.
gate_E_at :: Qubit -> Circ () Source #
Apply a Clifford E = HS3ω3 gate.
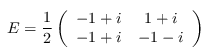
This gate is the unique Clifford operator with the properties E³ = I, EXE⁻¹ = Y, EYE⁻¹ = Z, and EZE⁻¹ = X. It is a convenient gate for calculations. For example, every Clifford operator can be uniquely written of the form
- EaXbScωd,
where a, b, c, and d are taken modulo 3, 2, 4, and 8, respectively.
gate_E_inv_at :: Qubit -> Circ () Source #
Apply the inverse of an E-gate.
gate_omega_at :: Qubit -> Circ () Source #
Apply the scalar ω = eiπ/4, as a single-qubit gate.
gate_V_at :: Qubit -> Circ () Source #
Apply a V = √X gate. This is by definition the following gate (see also Nielsen and Chuang, p.182):
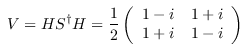
gate_V_inv_at :: Qubit -> Circ () Source #
Apply the inverse of a V-gate.
expZt_at :: Timestep -> Qubit -> Circ () Source #
Apply an e−iZt gate. The timestep t is a parameter.
gate_W_at :: Qubit -> Qubit -> Circ () Source #
Apply a W gate. The W gate is self-inverse and diagonalizes the SWAP gate.
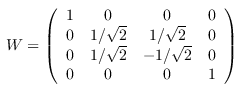
The arguments are such that
gate_W |0〉 |0〉 = |00〉 gate_W |0〉 |1〉 = (|01〉+|10〉) / √2 gate_W |1〉 |0〉 = (|01〉-|10〉) / √2 gate_W |1〉 |1〉 = |11〉.
In circuit diagrams, W1 denotes the "left" qubit, and W2 denotes the "right" qubit.
gate_iX_at :: Qubit -> Circ () Source #
Apply an iX gate. This gate is used similarly to the Pauli X gate, but with two advantages:
- the doubly-controlled iX gate can be implemented in the Clifford+T gate base with T-count 4 (the doubly-controlled X gate requires T-count 7);
- the iX-gate has determinant 1, and therefore an n-times controlled iX gate can be implemented in the Clifford+T gate base with no ancillas.
In particular, the iX gate can be used to implement an additional control with T-count 8, like this:

gate_iX_inv_at :: Qubit -> Circ () Source #
Apply a −iX gate. This is the inverse of gate_iX_at.
qmultinot_at :: QData qa => qa -> Circ () Source #
Negate all qubits in a quantum data structure.
swap_at :: QCData qc => qc -> qc -> Circ () Source #
Apply a swap gate to two qubits. More generally, apply swap gates to every corresponding pair of qubits in two pieces of quantum data.
Gates for state preparation and termination
qinit :: QShape ba qa ca => ba -> Circ qa Source #
Initialize a qubit from a boolean parameter. More generally, initialize a data structure of qubits from a corresponding data structure of boolean parameters. Examples:
q <- qinit False (q0, q1) <- qinit (True, False) [q0, q1, q2] <- qinit [True, False, True]
qterm :: QShape ba qa ca => ba -> qa -> Circ () Source #
Terminate a qubit, asserting its state to equal the boolean parameter. More generally, terminate a data structure of qubits, asserting that their state is as given by a data structure of booleans parameters. Examples:
qterm False q qterm (False, False) (q0, q1) qterm [False, False, False] [q0, q1, q2]
In some cases, it is permissible for some aspect of the parameter's shape to be underspecified, e.g., a longer than necessary list, or an integer of indeterminate length. It is therefore possible, for example, to write:
qterm 17 qa -- when qa :: QDInt, qterm [False..] qa -- when qa :: [Qubit].
The rules for when a boolean argument can be "promoted" in this way are specific to each individual data type.
qdiscard :: QData qa => qa -> Circ () Source #
Discard a qubit, ignoring its state. This can leave the quantum system in a mixed state, so is not a reversible operation. More generally, discard all the qubits in a quantum data structure. Examples:
qdiscard q qdiscard (q0, q1) qdiscard [q0, q1, q2]
cterm :: QShape ba qa ca => ba -> ca -> Circ () Source #
Terminate a Bit, asserting its state to equal the given
Bool. More generally, terminate a data structure of Bits,
asserting that their state is as given by a data structure of
Bools. Examples:
cterm False b cterm (False, False) (b0, b1) cterm [False, False, False] [b0, b1, b2]
In some cases, it is permissible for some aspect of the parameter's shape to be underspecified, e.g., a longer than necessary list, or an integer of indeterminate length. It is therefore possible, for example, to write:
cterm 17 ca -- when ca :: CInt, cterm [False..] ca -- when ca :: [Bit].
The rules for when a boolean argument can be "promoted" in this way are specific to each individual data type.
cdiscard :: CData ca => ca -> Circ () Source #
Discard a Bit, ignoring its state. This can leave the system in
a mixed state, so is not a reversible operation. More generally,
discard all the Bits in a data structure. Examples:
cdiscard b cdiscard (b0, b1) cdiscard [b0, b1, b2]
qc_init :: QCData qc => BType qc -> Circ qc Source #
Heterogeneous version of qinit. Please note that the type of
the result of this function cannot be inferred from the type of the
argument. For example,
x <- qc_init False
is ambiguous, unless it can be inferred from the context whether
x is a Bit or a Qubit. If the type cannot be inferred from
the context, it needs to be stated explicitly, like this:
x <- qc_init False :: Circ Qubit
Alternatively, qc_init_with_shape can be used to fix a specific
type.
qc_init_with_shape :: QCData qc => qc -> BType qc -> Circ qc Source #
A version of qc_init that uses a shape type parameter. The
first argument is the shape type parameter, and the second argument
is a data structure containing boolean initializers. The shape type
argument determines which booleans are used to initialize qubits,
and which ones are used to initialize classical bits.
Example:
(x,y) <- qc_init_with_shape (bit,[qubit]) (True, [False,True])
This will assign to x a classical bit initialized to 1, and to y a list of two qubits initialized to |0〉 and |1〉, respectively.
qc_measure :: QCData qc => qc -> Circ (QCType Bit Bit qc) Source #
Heterogeneous version of measure. Given a heterogeneous data
structure, measure all of its qubits, and leave any classical bits
unchanged.
qc_prepare :: QCData qc => qc -> Circ (QCType Qubit Qubit qc) Source #
Heterogeneous version of prepare. Given a heterogeneous data
structure, prepare qubits from all classical bits, and leave any
qubits unchanged.
Gates for classical circuits
The gates in this section are for constructing classical circuits. None of these gates alter or discard their inputs; each gate produces a new wire holding the output of the gate.
cgate_eq :: Bit -> Bit -> Circ Bit Source #
Test equality of two bits, and return True iff they are equal.
cgate_if :: CData ca => Bit -> ca -> ca -> Circ ca Source #
If a is True, return a copy of b, else return a copy of
c. Here b and c can be any data structures consisting of
Bits, but b and c must be of the same type and shape (for
example, if they are lists, they must be of equal
length). Examples:
output <- cgate_if a b c (out0, out1) <- cgate_if a (b0, b1) (c0, c1) [out0, out1, out2] <- cgate_if a [b0, b1, b2] [c0, c1, c2]
circ_if :: CData ca => Bit -> Circ ca -> Circ ca -> Circ ca Source #
circ_if is an if-then-else function for classical circuits.
It is a wrapper around cgate_if, intended to be used like this:
result <- circ_if <<<condition>>> ( <<then-part>>> )( <<<else-part>>> )
Unlike cgate_if, this is a meta-operation, i.e., the bodies of
the "then" and "else" parts can be circuit building
operations.
What makes this different from the usual boolean "if-then-else"
is that the condition is of type Bit, i.e., it is only known at
circuit execution time. Therefore the generated circuit contains
both the "then" and "else" parts, suitably
controlled. Precondition: the "then" and "else" parts must be
of the same type and shape.
User-defined gates
named_gate :: QData qa => String -> qa -> Circ qa Source #
Define a new functional-style gate of the given name. Usage:
my_unary_gate :: Qubit -> Circ Qubit my_unary_gate = named_gate "Q"
my_binary_gate :: (Qubit, Qubit) -> Circ (Qubit, Qubit) my_binary_gate = named_gate "R"
This defines a new unary gate and a new binary gate, which will be rendered as Q and R, respectively, in circuit diagrams.
named_gate_at :: QData qa => String -> qa -> Circ () Source #
Define a new imperative-style gate of the given name. Usage:
my_unary_gate_at :: Qubit -> Circ () my_unary_gate_at = named_gate_at "Q"
my_binary_gate_at :: (Qubit, Qubit) -> Circ () my_binary_gate_at = named_gate_at "R"
This defines a new unary gate and a new binary gate, which will be rendered as Q and R, respectively, in circuit diagrams.
named_rotation :: QData qa => String -> Timestep -> qa -> Circ qa Source #
Define a new functional-style gate of the given name, and parameterized by a real-valued parameter. This is typically used for rotations or phase gates that are parameterized by an angle. The name can contain '%' as a place holder for the parameter. Usage:
my_unary_gate :: Qubit -> Circ Qubit my_unary_gate = named_rotation "exp(-i%Z)" 0.123
my_binary_gate :: TimeStep -> (Qubit, Qubit) -> Circ (Qubit, Qubit) my_binary_gate t = named_rotation "Q(%)" t
named_rotation_at :: QData qa => String -> Timestep -> qa -> Circ () Source #
Define a new imperative-style gate of the given name, and parameterized by a real-valued parameter. This is typically used for rotations or phase gates that are parameterized by an angle. The name can contain '%' as a place holder for the parameter. Usage:
my_unary_gate_at :: Qubit -> Circ () my_unary_gate_at = named_rotation "exp(-i%Z)" 0.123
my_binary_gate_at :: TimeStep -> (Qubit, Qubit) -> Circ () my_binary_gate_at t = named_rotation "Q(%)" t
extended_named_gate :: (QData qa, QData qb) => String -> qa -> qb -> Circ qa Source #
Define a new functional-style gate of the given name. Like
named_gate, except that the generated gate is extended with
"generalized controls". The generalized controls are additional
inputs to the gate that are guaranteed not to be modified if they
are in a computational basis state. They are rendered in a special
way in circuit diagrams. Usage:
my_new_gate :: (Qubit,Qubit) -> Qubit -> Circ (Qubit,Qubit) my_new_gate = extended_named_gate "Q"
This defines a new gate with name Q, two inputs, and one generalized input.
extended_named_gate_at :: (QData qa, QData qb) => String -> qa -> qb -> Circ () Source #
Like extended_named_gate, except defines an imperative style gate.
Usage:
my_new_gate_at :: (Qubit,Qubit) -> Qubit -> Circ () my_new_gate_at = extended_named_gate_at "Q"
This defines a new gate with name Q, two inputs, and one generalized input.
Dynamic lifting
dynamic_lift :: QShape ba qa ca => ca -> Circ ba Source #
Convert a Bit (boolean circuit output) to a Bool (boolean
parameter). More generally, convert a data structure of Bits to a
corresponding data structure of Bools.
For use in algorithms that require the output of a measurement to be used as a circuit-generation parameter. This is the case, for example, for sieving methods, and also for some iterative algorithms.
Note that this is not a gate, but a meta-operation. The input consists of classical circuit endpoints (whose values are known at circuit execution time), and the output is a boolean parameter (whose value is known at circuit generation time).
The use of this operation implies an interleaving between circuit
execution and circuit generation. It is therefore a (physically)
expensive operation and should be used sparingly. Using the
dynamic_lift operation interrupts the batch mode operation of the
quantum device (where circuits are generated ahead of time), and
forces interactive operation (the quantum device must wait for the
next portion of the circuit to be generated). This operation is
especially expensive if the current circuit contains unmeasured
qubits; in this case, the qubits must be preserved while the
quantum device remains on standby.
Also note that this operation is not supported in all contexts. It is an error, for example, to use this operation in a circuit that is going to be reversed, or in the body of a boxed subroutine. Also, not all output devices (such as circuit viewers) support this operation.
Other circuit-building functions
qinit_of_char :: Char -> Circ Qubit Source #
Generate a new qubit initialized to one of |0〉, |1〉, |+〉, |−〉, depending on a character c which is '0', '1', '+', or '-'.
qinit_of_string :: String -> Circ [Qubit] Source #
Generate a list of qubits initialized to a sequence of |0〉, |1〉, |+〉, |−〉, defined by a string argument e.g. "00+0+++".
map_hadamard :: QData qa => qa -> Circ qa Source #
Apply a Hadamard gate to every qubit in a quantum data structure.
map_hadamard_at :: QData qa => qa -> Circ () Source #
Imperative version of map_hadamard.
controlled_not :: QCData qc => qc -> qc -> Circ (qc, qc) Source #
Apply a controlled-not gate to every corresponding pair of quantum or classical bits in two pieces of QCData. The first argument is the target and the second the (positive) control.
For now, we require both pieces of QCData to have the same type, i.e., classical bits can be controlled only by classical bits and quantum bits can be controlled only by quantum bits.
Example:
((a',b'), (x,y)) <- controlled_not (a,b) (x,y)
is equivalent to
a' <- qnot a `controlled` x b' <- qnot b `controlled` y
controlled_not_at :: QCData qc => qc -> qc -> Circ () Source #
Imperative version of controlled_not. Apply a controlled-not
gate to every corresponding pair of quantum or classical bits in
two pieces of QCData. The first argument is the target and the
second the (positive) control.
bool_controlled_not :: QCData qc => qc -> BType qc -> Circ qc Source #
A version of controlled_not where the control consists of
boolean data. Example:
bool_controlled_not (q, r, s) (True, True, False)
negates q and r, but not s.
bool_controlled_not_at :: QCData qc => qc -> BType qc -> Circ () Source #
A version of controlled_not_at where the control consists of
boolean data. Example:
bool_controlled_not_at (q, r, s) (True, True, False)
negates q and r, but not s.
qc_copy :: QCData qc => qc -> Circ qc Source #
Create a fresh copy of a piece of quantum data. Note: copying is
performed via a controlled-not operation, and is not cloning. This
is similar to qc_copy_fun, except it returns only the copy, and not
the original.
qc_uncopy :: QCData qc => qc -> qc -> Circ () Source #
"Uncopy" a piece of quantum data; i.e. terminate copy,
assuming it's a copy of orig. This is the inverse of
qc_copy, in the sense that the following sequence of
instructions behaves like the identity function:
b <- qc_copy a qc_uncopy a b
qc_copy_fun :: QCData qc => qc -> Circ (qc, qc) Source #
Initialize a new piece of quantum data, as a copy of a given piece. Returns both the original and the copy.
qc_uncopy_fun :: QCData qc => qc -> qc -> Circ qc Source #
Given two pieces of quantum data, assumed equal (w.r.t. the
computational basis), terminate the second piece (and return the
first, unmodified). This is the inverse of qc_copy_fun, in the sense
that the following sequence of instructions behaves like the
identity function:
(orig, copy) <- qc_copy_fun orig orig <- qc_uncopy_fun orig copy
mapUnary :: QData qa => (Qubit -> Circ Qubit) -> qa -> Circ qa Source #
Map a single qubit gate across every qubit in the data structure.
mapBinary :: QData qa => (Qubit -> Qubit -> Circ (Qubit, Qubit)) -> qa -> qa -> Circ (qa, qa) Source #
Map a binary gate across every corresponding pair of qubits in two quantum data structures of equal shape.
mapBinary_c :: QShape ba qa ca => (Qubit -> Bit -> Circ (Qubit, Bit)) -> qa -> ca -> Circ (qa, ca) Source #
Like mapBinary, except the second data structure is classical.
qc_mapBinary :: QCData qc => (Qubit -> Qubit -> Circ (Qubit, Qubit)) -> (Bit -> Bit -> Circ (Bit, Bit)) -> qc -> qc -> Circ (qc, qc) Source #
Heterogeneous version of mapBinary. Map a binary gate f
across every corresponding pair of qubits, and a binary gate g
across every corresponding pair of bits, in two quantum data
structures of equal shape.
Notation for controls
Some gates can be controlled by a condition involving one of more "control" qubits and/or classical bits at circuit execution time. Such gates can also be controlled by boolean conditions that are known at circuit generation time (in which case the gate will not be generated when the control condition is false). This section provides a convenient and flexible syntax for specifying controls.
In Quipper, controls can be written in a way that is reminiscent of (a restricted set of) ordinary boolean expressions. Here are some examples:
q1 .==. 0 .&&. q2 .==. 1 for Qubits q1, q2
q .&&. p means q .==. 1 .&&. p .==. 1
qx .==. 5 for a QDInt qx
q1 .==. 0 .&&. z <= 7 combines quantum and classical controls
q ./=. b the negation of q .==. b;
here b is a boolean.[p,q,r,s] a list of positive controls
[Signed p True, Signed q False, Signed r False, Signed s True]
a list of positive and negative controlsAmong these infix operators, (.&&.) binds more weakly than
(.==.), (./=.).
Controls can be attached to a gate by means of the infix
operator controlled:
gate `controlled` <<controls>>
class ControlSource a where Source #
A "control source" is anything that can be used as a control on
a gate. The most common way to construct a control source is by
using the .==., ./=., and .&&.
operators. In addition, we provide the following instances:
Bool. A boolean condition that is known at circuit generation time can be used as a control, which is then either trivial (the gate is generated) or inconsistent (the gate is not generated).Wire. This includes the typeBit(for a classical execution-time control) andQubit(for a quantum control). A wire can be used as a shorthand notation for a positive control on that wire.ControlList. A control list is Quipper's internal representation of a control condition, and is trivially a control source.- A list of control sources can be used as a control source.
Instances
data ControlList Source #
A ControlList is Quipper's internal representation of the type
of conjunctive controls, i.e., controls that can be constructed
using the .==., ./=., and .&&.
operators.
Instances
| Show ControlList # | |
Defined in Quipper.Internal.Control Methods showsPrec :: Int -> ControlList -> ShowS # show :: ControlList -> String # showList :: [ControlList] -> ShowS # | |
| ControlSource ControlList # | |
Defined in Quipper.Internal.Control Methods to_control :: ControlList -> ControlList Source # | |
(.&&.) :: (ControlSource a, ControlSource b) => a -> b -> ControlList infixr 3 Source #
This is an infix operator to concatenate two controls, forming their logical conjunction.
(.==.) :: QCData qc => qc -> BType qc -> ControlList infix 4 Source #
(qx .==. x): a control which is true just if quantum data qx is in the specified state x.
controlled :: ControlSource c => Circ a -> c -> Circ a infixl 2 Source #
An infix operator to apply the given controls to a gate:
gate `controlled` <<controls>>
It also works with functional-style gates:
result <- gate `controlled` <<controls>>
The infix operator is left associative, so it can be applied multiple times:
result <- gate `controlled` <<controls1>> `controlled` <<controls2>>
The latter is equivalent to
result <- gate `controlled` <<controls1>> .&&. <<controls2>>
Signed items
A signed item of type a. Signed x True represents a
positive item, and Signed x False represents a negative item.
When used with wires in a circuit, a positive sign is used to represent a positive control, i.e., a filled dot, and a negative sign is used to represent a negative control, i.e., an empty dot.
Instances
from_signed :: Signed a -> a Source #
Extract the underlying item of a signed item.
Comments and labelling
comment :: String -> Circ () Source #
Insert a comment in the circuit. This is not a gate, and has no effect, except to mark a spot in the circuit. How the comment is displayed depends on the printing backend.
label :: Labelable qa labels => qa -> labels -> Circ () Source #
Label qubits in the circuit. This is not a gate, and has no effect, except to make the circuit more readable. How the labels are displayed depends on the printing backend. This can take several different forms. Examples:
Label q as q and r as r:
label (q,r) ("q", "r")Label a, b, and c as a, b, and c, respectively:
label [a,b,c] ["a", "b", "c"]
Label q as x[0] and r as x[1]:
label (q,r) "x"
Label a, b, and c as x[0], x[1], x[2]:
label [a,b,c] "x"
without_comments :: Circ a -> Circ a Source #
Disable labels and comments for a block of code. The intended usage is like this:
without_comments $ do {
<<<code block>>>
}This is sometimes useful in situations where code is being re-used, for example when one function is implemented in terms of another, but should not inherit comments from it. It is also useful in the definition of recursive function, where a comment should only be applied at the outermost level. Finally, it can be used to suppress comments from parts of circuits for presentation purposes.
Labelable a s means that a is a data structure that can
be labelled with the format s. A "format" is a string, or a
data structure with strings at the leaves.
Minimal complete definition
Instances
Hierarchical circuits
box :: (QCData qa, QCData qb, QCurry qa_qb qa qb) => String -> qa_qb -> qa_qb Source #
A generic interface for wrapping a circuit-generating function into a boxed and named subroutine. This takes a name and a circuit-generating function, and returns a new circuit-generating function of the same type, but which inserts a boxed subroutine instead of the actual body of the subroutine.
It is intended to be used like this:
somefunc :: Qubit -> Circ Qubit somefunc a = do ... somefunc_boxed :: Qubit -> Circ Qubit somefunc_boxed = box "somefunc" somefunc
Here, the type of somefunc is just an example; this could indeed
be a function with any number and type of arguments, as long as the
arguments and return type are quantum data.
It is also possible to inline the box operator directly, in which
case it should be done like this:
somefunc :: Qubit -> Circ Qubit somefunc = box "somefunc" $ \a -> do ...
Note: The box operator wraps around a complete function,
including all of its arguments. It would be incorrect to apply the
box operator after some quantum variables have already been
defined. Thus, the following is incorrect:
incorrect_somefunc :: Qubit -> Circ Qubit incorrect_somefunc a = box "somefunc" $ do ...
It is the user's responsibility not to use the same name for
different subroutines. If box is called more than once with the
same name and shape of input, Quipper assumes, without checking,
that they are subsequent calls to the same subroutine.
The type of the box operator is overloaded and quite difficult to
read. It can have for example the following types:
box :: String -> (Qubit -> Circ Qubit) -> (Qubit -> Circ Qubit) box :: String -> (QDInt -> QDInt -> Circ (QDInt,QDInt,QDInt)) -> (QDInt -> QDInt -> Circ (QDInt,QDInt,QDInt))
nbox :: QCData qa => String -> Integer -> (qa -> Circ qa) -> qa -> Circ qa Source #
A version of box with iteration. The second argument is an
iteration count.
This can only be applied to functions of a single argument, where the input and output types are the same.
box_loopM :: (Integral int, QCData qa) => String -> int -> qa -> (qa -> Circ qa) -> Circ qa Source #
loopM_boxed_if :: (Integral int, QCData qa) => Bool -> String -> int -> qa -> (qa -> Circ qa) -> Circ qa Source #
A version of loopM that will be boxed conditionally on a
boolean condition. Typical usage:
loopM_boxed_if (s > 1) "name" s x $ \x -> do <<<body>>> return x
Block structure
The following are higher-order functions that provide a way to structure quantum programs into blocks. A block can contain local ancillas or local controls.
Ancillas
The use of the with_ancilla family of operators is
preferable to using qinit and qterm directly. In particular, it
is possible to add controls to a block created with one of the
with_ancilla family of operators, whereas qinit and qterm,
when used individually, cannot be controlled.
with_ancilla :: (Qubit -> Circ a) -> Circ a Source #
Convenient wrapper around qinit and
qterm. This can be used to introduce an ancilla with a
local scope, like this:
with_ancilla $ \h -> do {
<<<code block using ancilla h>>>
}The ancilla will be initialized to |0〉 at the beginning of the block, and it is the programmer's responsibility to ensure that it will be returned to state |0〉 at the end of the block.
A block created with with_ancilla is controllable, provided that
the body is controllable.
with_ancilla_list :: Int -> (Qulist -> Circ a) -> Circ a Source #
Like with_ancilla, but creates a list of n ancillas, all
initialized to |0〉. Usage:
with_ancilla_list n $ \a -> do {
<<<code block using list of ancillas a>>>
}with_ancilla_init :: QShape a qa ca => a -> (qa -> Circ b) -> Circ b Source #
Execute a block with local ancillas. Opens a block, initializing an ancilla with a specified classical value, and terminates it with the same value when the block closes. Note: it is the programmer's responsibility to return the ancilla to its original state at the end of the enclosed block. Usage:
with_ancilla_init True $ \a -> do {
<<<code block using ancilla a initialized to True>>>
}with_ancilla_init [True,False,True] $ \a -> do {
<<<code block using list of ancillas a initialized to [True,False,True]>>>
}Automatic uncomputing
with_computed_fun :: (QCData x, QCData y) => x -> (x -> Circ y) -> (y -> Circ (y, b)) -> Circ (x, b) Source #
with_computed_fun x f g
Important subtlety in usage: all quantum data referenced in f, even as controls, must be explicitly bound and returned by f, or the reversing may rebind it incorrectly. g, on the other hand, can safely refer to anything that is in scope outside the with_computed_fun.
with_computed :: QCData x => Circ x -> (x -> Circ b) -> Circ b Source #
with_computed computation code
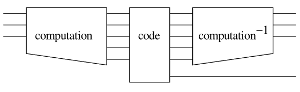
Both computation and code may refer to any qubits that exist in the current environment, and they may also create new qubits. computation may produce arbitrary garbage in addition to its output.
This is a very general but relatively unsafe operation. It is the user's responsibility to ensure that the computation can indeed be undone. In particular, if computation contains any initializations, then code must ensure that the corresponding assertions will be satisfied in computation−1.
Related more specialized, but potentially safer, operations are:
with_basis_change, which is likewith_computed, but assumes that computation is unitary, andclassical_to_reversible, which assumes that computation is classical (or pseudo-classical), and code is a simple copy-by-controlled-not operation.
with_basis_change :: Circ () -> Circ b -> Circ b Source #
with_basis_change basischange code
with_basis_change basischange $ do
<<<code>>>
where
basischange = do
<<<gates>>>Controls
with_controls :: ControlSource c => c -> Circ a -> Circ a Source #
A syntax for "if"-style (classical and quantum) controls. This can be used as follows:
gate1
with_controls <<controls>> $ do {
gate2
gate3
}
gate4The specified controls will be applied to gate2 and gate3. It is an error to specify a control for a gate that cannot be controlled (such as measurement).
with_classical_control :: QCData qa => Bit -> String -> qa -> (qa -> Circ qa) -> Circ qa Source #
Classical control on a function with same shape of input and output: if the control bit is true the function is fired, otherwise the identity map is used. Note: the constraint on the types is dynamically checked.
without_controls :: Circ a -> Circ a Source #
Apply a block of gates while temporarily suspending the
application of controls. This can be used to omit controls on
gates where they are known to be unnecessary. This is a relatively
low-level function and should not normally be called directly by
user code. Instead, it is safer to use a higher-level function such
as with_basis_change. However, the without_controls operator is
useful in certain situations, e.g., it can be used to preserve the
NoControlFlag when defining transformers.
Usage:
without_controls $ do <<code block>>
or:
without_controls (gate)
Note that all controls specified in the surrounding code are
disabled within the without_controls block. This is even true if
the without_controls block appears in a subroutine, and the
subroutine is later called in a controlled context. On the other
hand, it is possible to specify controls inside the
without_controls block. Consider this example:
my_subcircuit = do
gate1
without_controls $ do {
gate2
gate3 `controlled` <<controls1>>
}
gate4
my_circuit = do
my_subcircuit `controlled` <<controls2>>In this example, controls 1 will be applied to gate 3, controls 2 will be applied to gates 1 and 4, and no controls will be applied to gate 2.
without_controls_if :: NoControlFlag -> Circ a -> Circ a Source #
Apply without_controls if NoControlFlag is True, otherwise
do nothing.
Loops
for :: Monad m => Int -> Int -> Int -> (Int -> m ()) -> m () Source #
A "for" loop. Counts from a to b in increments of s.
Standard notation:
for i = a to b by s do commands end for
Our notation:
for a b s $ \i -> do commands endfor
endfor :: Monad m => m () Source #
Mark the end of a "for"-loop. This command actually does nothing, but can be used to make the loop look prettier.
foreach :: Monad m => [a] -> (a -> m b) -> m () Source #
Iterate a parameter over a list of values. It can be used as follows:
foreach [1,2,3,4] $ \n -> do <<<loop body depending on the parameter n>>> endfor
The loop body will get executed once for each n ∈ {1,2,3,4}.
loop :: (Eq int, Num int) => int -> t -> (t -> t) -> t Source #
Iterate a function n times. Example:
loop 3 x f = f (f (f x))
loop_with_index :: (Eq int, Num int) => int -> t -> (int -> t -> t) -> t Source #
Like loop, but also pass a loop counter to the function being
iterated. Example:
loop_with_index 3 x f = f 2 (f 1 (f 0 x))
loopM :: (Eq int, Num int, Monad m) => int -> t -> (t -> m t) -> m t Source #
Monadic version of loop.
loop_with_indexM :: (Eq int, Num int, Monad m) => int -> t -> (int -> t -> m t) -> m t Source #
Monadic version of loop_with_index. Thus,
loop_with_indexM 3 x0 f
will do the following:
do x1 <- f 0 x0 x2 <- f 1 x1 x3 <- f 2 x2 return x3
Operations on circuits
Reversing
reverse_generic :: (QCData x, QCData y, TupleOrUnary xt x, QCurry x_y x y, Curry x_y_xt x (y -> Circ xt)) => x_y -> x_y_xt Source #
Reverse a circuit-generating function. The reversed function requires a shape parameter, given as the input type of the original function.
The type of this highly overloaded function is quite difficult to read. It can have for example the following types:
reverse_generic :: (QCData x, QCData y) => (x -> Circ y) -> x -> (y -> Circ x) reverse_generic :: (QCData x, QCData y, QCData z) => (x -> y -> Circ z) -> x -> y -> (z -> Circ (x,y))
reverse_simple :: (QCData_Simple x, QCData y, TupleOrUnary xt x, QCurry x_y x y) => x_y -> y -> Circ xt Source #
Like reverse_generic, but only works at simple types, and
therefore requires no shape parameters. Typical type instances:
reverse_simple :: (QCData_Simple x, QCData y) => (x -> Circ y) -> (y -> Circ x) reverse_simple :: (QCData_Simple x, QCData_Simple y, QCData z) => (x -> y -> Circ z) -> (z -> Circ (x,y))
reverse_generic_endo :: (QCData x, TupleOrUnary xt x, QCurry x_xt x xt) => x_xt -> x_xt Source #
Like reverse_generic, but specialized to endomorphic circuits,
i.e., circuits where the input and output have the same type (modulo
possibly currying) and shape. In this case, unlike reverse_generic,
no additional shape parameter is required, and the reversed function
is curried if the original function was. Typical type instances:
reverse_generic_endo :: (QCData x) => (x -> Circ x) -> (x -> Circ x) reverse_generic_endo :: (QCData x, QCData y) => (x -> y -> Circ (x,y)) -> (x -> y -> Circ (x,y))
reverse_generic_imp :: (QCData x, QCurry x__ x ()) => x__ -> x__ Source #
Like reverse_generic_endo, but applies to endomorphic circuits
expressed in "imperative" style. Typical type instances:
reverse_generic_endo :: (QCData x) => (x -> Circ ()) -> (x -> Circ ()) reverse_generic_endo :: (QCData x, QCData y) => (x -> y -> Circ ()) -> (x -> y -> Circ ())
reverse_generic_curried :: (QCData x, QCData y, TupleOrUnary xt x, Tuple yt y, QCurry x_yt x yt, QCurry y_xt y xt, Curry x_y_xt x y_xt) => x_yt -> x_y_xt Source #
Like reverse_generic, but takes functions whose output is a
tuple, and curries the reversed function. Differs from
reverse_generic in an example such as:
f :: (x -> y -> Circ (z,w)) reverse_generic f :: x -> y -> ((z,w) -> Circ (x,y)) reverse_generic_curried f :: x -> y -> (z -> w -> Circ (x,y))
Note: the output must be a n-tuple, where n = 0 or n ≥
2. Applying this to a circuit whose output is a non-tuple type is a
type error; in this case, reverse_generic should be used.
reverse_simple_curried :: (QCData_Simple x, QCData y, TupleOrUnary xt x, Tuple yt y, QCurry x_yt x yt, QCurry y_xt y xt) => x_yt -> y_xt Source #
Like reverse_simple, but takes functions whose output is a
tuple, and curries the reversed function. Typical type instance:
reverse_simple_curried :: (QCData_Simple x, QCData y, QCData z) => (x -> Circ (y,z)) -> (y -> z -> Circ x)
Note: the output must be a n-tuple, where n = 0 or n ≥
2. Applying this to a circuit whose output is a non-tuple type is a
type error; in this case, reverse_generic should be used.
reverse_endo_if :: (QCData x, TupleOrUnary xt x, QCurry x_xt x xt) => Bool -> x_xt -> x_xt Source #
Conditional version of reverse_generic_endo. Invert the
endomorphic quantum circuit if the boolean is true; otherwise,
insert the non-inverted circuit.
reverse_imp_if :: (QCData qa, QCurry fun qa ()) => Bool -> fun -> fun Source #
Conditional version of reverse_generic_imp. Invert the
imperative style quantum circuit if the boolean is true; otherwise,
insert the non-inverted circuit.
Printing
Available output formats.
Constructors
| EPS | Encapsulated PostScript graphics. |
Portable Document Format. One circuit per page. | |
| PS | PostScript. One circuit per page. |
| ASCII | A textual representation of circuits. |
| Preview | Don't print anything, but preview directly on screen (requires the external program acroread). |
| GateCount | Print statistics on gate counts. |
| CustomStyle FormatStyle |
data FormatStyle Source #
A data type that holds all the customizable parameters.
Constructors
| FormatStyle | |
Fields
| |
Instances
| Show FormatStyle # | |
Defined in Quipper.Internal.Printing Methods showsPrec :: Int -> FormatStyle -> ShowS # show :: FormatStyle -> String # showList :: [FormatStyle] -> ShowS # | |
format_enum :: [(String, Format)] Source #
A mapping from lower-case strings (to be used, e.g., with command line options) to available formats.
print_unary :: QCData qa => Format -> (qa -> Circ b) -> qa -> IO () Source #
Print a circuit generating function to the specified format; this requires a shape parameter.
print_generic :: (QCData qa, QCurry qfun qa b, Curry fun qa (IO ())) => Format -> qfun -> fun Source #
Print a circuit generating function to the specified
format. Unlike print_unary, this can be applied to a
circuit-generating function in curried form with n arguments, for
any n >= 0. It then requires n shape parameters.
The type of this heavily overloaded function is difficult to read. In more readable form, it has all of the following types:
print_generic :: Format -> Circ qa -> IO () print_generic :: (QCData qa) => Format -> (qa -> Circ qb) -> a -> IO () print_generic :: (QCData qa, QCData qb) => Format -> (qa -> qb -> Circ qc) -> a -> b -> IO ()
and so forth.
print_simple :: (QCData qa, QCurry qfun qa b, Curry fun qa (IO ()), QCData_Simple qa) => Format -> qfun -> IO () Source #
Like print_generic, but only works at simple types, and
therefore requires no shape parameters.
print_of_document_custom :: Custom -> Format -> Document a -> IO a Source #
Like print_of_document, but also takes a Custom data
structure.
Classical circuits
classical_to_cnot :: (QCData qa, QCData qb, QCurry qfun qa qb) => qfun -> qfun Source #
Translate all classical gates in a circuit into equivalent controlled-not gates.
The type of this overloaded function is difficult to read. In more readable form, it has all of the following types:
classical_to_cnot :: (QCData qa) => Circ qa -> Circ qa classical_to_cnot :: (QCData qa, QCData qb) => (qa -> Circ qb) -> (qa -> Circ qb) classical_to_cnot :: (QCData qa, QCData qb, QCData qc) => (qa -> qb -> Circ qc) -> (qa -> qb -> Circ qc)
and so forth.
classical_to_quantum :: (QCData qa, QCData qb, QCurry qfun qa qb, QCurry qfun' (QType qa) (QType qb)) => qfun -> qfun' Source #
Replace all classical gates in a circuit by equivalent quantum gates.
The type of this overloaded function is difficult to read. In more readable form, it has all of the following types:
classical_to_quantum :: (QCData qa) => Circ qa -> Circ (QType qa) classical_to_quantum :: (QCData qa, QCData qb) => (qa -> Circ qb) -> (QType qa -> Circ (QType qb)) classical_to_quantum :: (QCData qa, QCData qb, QCData qc) => (qa -> qb -> Circ qc) -> (QType qa -> QType qb -> Circ (QType qc))
and so forth.
Ancilla uncomputation
classical_to_reversible :: (QCData qa, QCData qb) => (qa -> Circ qb) -> (qa, qb) -> Circ (qa, qb) Source #
Generic function for turning a classical (or pseudo-classical)
circuit into a reversible circuit. The input is a classical boolean
function x ↦ f(x), given as a not necessarily reversible
circuit (however, the circuit should be one-to-one, i.e., no
"garbage" should be explicitly erased). The output is the
corresponding reversible function (x,y) ↦ (x,y ⊕
f(x)). qa and qb can be any quantum data types. The
function classical_to_reversible does not itself change
classical bits to qubits; use classical_to_quantum for that.
Circuit transformers
Transformers are a very general way of defining mappings over circuits. Possible uses of this include:
- gate transformations, where a whole circuit is transformed by replacing each kind of gate with another gate or circuit;
- error correcting codes, where a whole circuit is transformed replacing each qubit by some fixed number of qubits, and each gate by a circuit; and
- simulations, where a whole circuit is mapped to a semantic function by specifying a semantic function for each gate.
The interface is designed to allow the programmer to specify new transformers easily. To define a specific transformation, the programmer has to specify only three pieces of information:
- Types a=⟦Qubit⟧ and b=⟦Bit⟧, to serve as semantic domains.
- A monad m. This is to allow translations to have side effects if desired; one can use the identity monad otherwise.
- For every gate G, a corresponding semantic function ⟦G⟧. The type of this function depends on what kind of gate G is. For example:
If G :: Qubit -> Circ Qubit, then ⟦G⟧ :: a -> m a. If G :: (Qubit, Bit) -> Circ (Bit, Bit), then ⟦G⟧ :: (a, b) -> m (b, b).
The programmer provides this information by defining a function of
type Transformer m a b, see below. Once a
particular transformer has been defined, it can then be applied to
entire circuits. For example, for a circuit with 1 inputs and 2
outputs:
If C :: Qubit -> (Qubit, Qubit), then ⟦C⟧ :: a -> m (a, a).
User-definable transformers
type Transformer m a b = forall x. T_Gate m a b x -> x Source #
A circuit transformer is specified by defining a function of type
Transformer m a b. This involves specifying a monad m,
semantic domains a=⟦Qubit⟧ and b=⟦Bit⟧, and a semantic function
for each gate, like this:
my_transformer :: Transformer m a b my_transformer (T_Gate1 <parameters> f) = f $ <semantic function for gate 1> my_transformer (T_Gate2 <parameters> f) = f $ <semantic function for gate 2> my_transformer (T_Gate3 <parameters> f) = f $ <semantic function for gate 3> ...
The type T_Gate is used to define case distinctions over gates
in the definition of transformers. For each kind of gate X, it
contains a constructor of the form (T_X f). Here, X identifies
the gate, and f is a higher-order function to pass the
translation of X to.
Constructors
Pre-defined transformers
identity_transformer :: Transformer Circ Qubit Bit Source #
The identity transformer. This just maps a low-level circuits to the corresponding circuit-generating function. It can also be used as a building block in other transformers, to define "catch-all" clauses for gates that don't need to be transformed.
An example transformer
The following is a short but complete example of how to write and use a simple transformer. As usual, we start by importing Quipper:
import Quipper
We will write a transformer called sample_transformer, which maps
every swap gate to a sequence of three controlled-not gates, and
leaves all other gates unchanged. For convenience, Quipper
pre-defines an identity_transformer, which can be used as a
catch-all clause to take care of all the gates that don't need to
be rewritten.
mytransformer :: Transformer Circ Qubit Bit
mytransformer (T_QGate "swap" 2 0 _ ncf f) = f $
\[q0, q1] [] ctrls -> do
without_controls_if ncf $ do
with_controls ctrls $ do
qnot_at q0 `controlled` q1
qnot_at q1 `controlled` q0
qnot_at q0 `controlled` q1
return ([q0, q1], [], ctrls)
mytransformer g = identity_transformer gNote how Quipper syntax has been used to define the replacement
circuit new_swap, consisting of three controlled-not gates. Also,
since the original swap gate may have been controlled, we have
added the additional controls with a with_controls
operator. Finally, the without_controls_if operator ensures that
if the NoControlFlag is set on the original swap gate, then it
will also be set on the replacement circuit.
To try this out, we define some random circuit using swap gates:
mycirc a b c d = do swap_at a b hadamard_at b swap_at b c `controlled` [a, d] hadamard_at c swap_at c d
To apply the transformer to this circuit, we use the generic
operator transform_generic:
mycirc2 = transform_generic mytransformer mycirc
Finally, we use a main function to display the original circuit
and then the transformed one:
main = do print_simple Preview mycirc print_simple Preview mycirc2
Applying transformers to circuits
transform_generic :: (QCData x, QCData y, QCurry qfun x y) => Transformer Circ Qubit Bit -> qfun -> qfun Source #
Apply the given transformer to a circuit. Unlike
transform_unary, this function can be applied to a
circuit-generating function in curried form with n arguments, for
any n ≥ 0.
The type of this heavily overloaded function is difficult to read. In more readable form, it has all of the following types:
transform_generic :: (QCData x) => Transformer Circ Qubit Bit -> Circ x -> Circ x transform_generic :: (QCData x, QCData y) => Transformer Circ Qubit Bit -> (x -> Circ y) -> (x -> Circ y) transform_generic :: (QCData x, QCData y, QCData z) => Transformer Circ Qubit Bit -> (x -> y -> Circ z) -> (x -> y -> Circ z)
and so forth.
transform_generic_shape :: (QCData x, QCData y, QCurry qfun x y, Curry qfun' x' (m y'), Curry qfun'' x qfun', x' ~ QCType a b x, y' ~ QCType a b y, Monad m) => Transformer m a b -> qfun -> qfun'' Source #
Like transform_generic, but applies to arbitrary transformers
of type
Transformer m a b
instead of the special case
Transformer Circ Qubit Bit.
This requires an additional shape argument.
The type of this heavily overloaded function is difficult to read. In more readable form, it has all of the following types:
transform_generic :: (QCData x) => Transformer m a b -> Circ x -> m (QCData a b x) transform_generic :: (QCData x, QCData y) => Transformer m a b -> (x -> Circ y) -> x -> (QCData a b x -> m (QCData a b y)) transform_generic :: (QCData x, QCData y, QCData z) => Transformer m a b -> (x -> y -> Circ z) -> x -> y -> (QCData a b x -> QCData a b y -> m (QCData a b z))
and so forth.
Auxiliary type definitions
type InverseFlag = Bool Source #
A flag that, if True, indicates that the gate is inverted.
type NoControlFlag = Bool Source #
A flag that, if True, indicates that the gate is controllable,
but any further controls on the gate should be ignored. This is
used, e.g., for circuits consisting of a basis change, some
operation, and the inverse basis change. When controlling such a
circuit, it is sufficient to control the middle operation, so the
gates belonging to the basis change and its inverse will have the
NoControlFlag set.
data B_Endpoint a b Source #
An endpoint is either a qubit or a bit. In a transformer,
we have ⟦B_Endpoint Qubit Bit⟧ = ⟦Qubit⟧ + ⟦Bit⟧. The type B_Endpoint
a b is the same as Either a b, but we use more suggestive
field names.
Constructors
| Endpoint_Qubit a | |
| Endpoint_Bit b |
Instances
type Ctrls a b = [Signed (B_Endpoint a b)] Source #
A list of signed values of type ⟦B_Endpoint⟧. This type is an abbreviation defined for convenience.
Automatic circuit generation from classical code
The following two modules provide functions that are useful for automatic circuit generation from classical code. Please see Quipper.Internal.CircLifting for a more detailed explanation of how to use this feature.
module Quipper.Internal.CircLifting
module Quipper.Utils.Template
Extended quantum data types
Homogeneous quantum data types
type QShape ba qa ca = (QData qa, BType qa ~ ba, CType qa ~ ca) Source #
The QShape class allows the definition of generic functions that
can operate on quantum data of any "shape", for example, nested
tuples or lists of qubits.
In general, there are three kinds of data: quantum inputs (such as
Qubit), classical inputs (such as Bit), and classical
parameters (such as Bool). For example, a Qubit can be
initialized from a Bool; a Qubit can be measured, resulting in
a Bit, etc. For this reason, the type class QShape establishes a
relation between three types:
qa- A data structure having
Qubitat the leaves. ca- A data structure of the same shape as
qa, havingBitat the leaves. ba- A data structure of the same shape as
qa, havingBoolat the leaves.
Some functions input a classical parameter for the sole purpose of establishing the "shape" of a piece of data. The shape refers to qualities of a data structure, such as the length of a list, which are not uniquely determined by the type. For example, two different lists of length 5 have the same shape. When performing a generic operation, such as reversing a circuit, it is often necessary to specify the shape of the inputs, but not the actual inputs.
In the common case where one only needs to declare one of the types
qa, ca, or ba, one of the simpler type classes QData,
CData, or BData can be used.
type QData qa = (qa ~ QType (CType qa), qa ~ QTypeB (BType qa), qa ~ QCType Qubit Bool qa, qa ~ QType qa, QCData qa, QCData (CType qa)) Source #
Heterogeneous quantum data types
class (Labelable qc String, Typeable qc, Show qc, Show (LType qc), qc ~ QCType Qubit Bit qc, CType (QType qc) ~ CType qc, BType (CType qc) ~ BType qc, QCType Int Bool (CType qc) ~ BType qc) => QCData qc Source #
The QCData type class contains heterogeneous data types built
up from leaves of type Qubit and Bit. It is the basis for
several generic operations that apply to classical and quantum
data, such as copying, transformers, simulation, and heterogeneous
versions of qterm and qdiscard.
QCData and QData are interrelated, in the sense that the
following implications hold:
QData qa implies QCData qa CData ca implies QCData ca
Implications in the converse direction also hold whenever qc is a fixed known type:
QCData qc implies QData (QType qc) QCData qc implies CData (CType qc) QCData qc implies BData (BType qc)
However, the type checker cannot prove the above implication in the
case where qc is a type variable; for this, the more flexible
(but more computationally expensive) QCDataPlus class can be used.
Minimal complete definition
Instances
| QCData Char # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Char -> (q -> m q') -> (c -> m c') -> QCType q c Char -> m (QCType q' c' Char) Source # qcdata_zip :: Char -> q -> c -> q' -> c' -> QCType q c Char -> QCType q' c' Char -> ErrMsg -> QCType (q, q') (c, c') Char Source # qcdata_promote :: BType Char -> Char -> ErrMsg -> BType Char Source # | |
| QCData Double # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Double -> (q -> m q') -> (c -> m c') -> QCType q c Double -> m (QCType q' c' Double) Source # qcdata_zip :: Double -> q -> c -> q' -> c' -> QCType q c Double -> QCType q' c' Double -> ErrMsg -> QCType (q, q') (c, c') Double Source # qcdata_promote :: BType Double -> Double -> ErrMsg -> BType Double Source # | |
| QCData Float # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Float -> (q -> m q') -> (c -> m c') -> QCType q c Float -> m (QCType q' c' Float) Source # qcdata_zip :: Float -> q -> c -> q' -> c' -> QCType q c Float -> QCType q' c' Float -> ErrMsg -> QCType (q, q') (c, c') Float Source # qcdata_promote :: BType Float -> Float -> ErrMsg -> BType Float Source # | |
| QCData Int # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Int -> (q -> m q') -> (c -> m c') -> QCType q c Int -> m (QCType q' c' Int) Source # qcdata_zip :: Int -> q -> c -> q' -> c' -> QCType q c Int -> QCType q' c' Int -> ErrMsg -> QCType (q, q') (c, c') Int Source # qcdata_promote :: BType Int -> Int -> ErrMsg -> BType Int Source # | |
| QCData Integer # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Integer -> (q -> m q') -> (c -> m c') -> QCType q c Integer -> m (QCType q' c' Integer) Source # qcdata_zip :: Integer -> q -> c -> q' -> c' -> QCType q c Integer -> QCType q' c' Integer -> ErrMsg -> QCType (q, q') (c, c') Integer Source # qcdata_promote :: BType Integer -> Integer -> ErrMsg -> BType Integer Source # | |
| QCData () # | |
Defined in Quipper.Internal.QData | |
| QCData Bit # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Bit -> (q -> m q') -> (c -> m c') -> QCType q c Bit -> m (QCType q' c' Bit) Source # qcdata_zip :: Bit -> q -> c -> q' -> c' -> QCType q c Bit -> QCType q' c' Bit -> ErrMsg -> QCType (q, q') (c, c') Bit Source # qcdata_promote :: BType Bit -> Bit -> ErrMsg -> BType Bit Source # | |
| QCData Qubit # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Qubit -> (q -> m q') -> (c -> m c') -> QCType q c Qubit -> m (QCType q' c' Qubit) Source # qcdata_zip :: Qubit -> q -> c -> q' -> c' -> QCType q c Qubit -> QCType q' c' Qubit -> ErrMsg -> QCType (q, q') (c, c') Qubit Source # qcdata_promote :: BType Qubit -> Qubit -> ErrMsg -> BType Qubit Source # | |
| QCData a => QCData [a] # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => [a] -> (q -> m q') -> (c -> m c') -> QCType q c [a] -> m (QCType q' c' [a]) Source # qcdata_zip :: [a] -> q -> c -> q' -> c' -> QCType q c [a] -> QCType q' c' [a] -> ErrMsg -> QCType (q, q') (c, c') [a] Source # qcdata_promote :: BType [a] -> [a] -> ErrMsg -> BType [a] Source # | |
| QCData a => QCData (Signed a) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => Signed a -> (q -> m q') -> (c -> m c') -> QCType q c (Signed a) -> m (QCType q' c' (Signed a)) Source # qcdata_zip :: Signed a -> q -> c -> q' -> c' -> QCType q c (Signed a) -> QCType q' c' (Signed a) -> ErrMsg -> QCType (q, q') (c, c') (Signed a) Source # qcdata_promote :: BType (Signed a) -> Signed a -> ErrMsg -> BType (Signed a) Source # | |
| (QCData a, QCData b) => QCData (a, b) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b) -> (q -> m q') -> (c -> m c') -> QCType q c (a, b) -> m (QCType q' c' (a, b)) Source # qcdata_zip :: (a, b) -> q -> c -> q' -> c' -> QCType q c (a, b) -> QCType q' c' (a, b) -> ErrMsg -> QCType (q, q') (c, c') (a, b) Source # qcdata_promote :: BType (a, b) -> (a, b) -> ErrMsg -> BType (a, b) Source # | |
| (QCData a, QCData b) => QCData (B_Endpoint a b) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => B_Endpoint a b -> (q -> m q') -> (c -> m c') -> QCType q c (B_Endpoint a b) -> m (QCType q' c' (B_Endpoint a b)) Source # qcdata_zip :: B_Endpoint a b -> q -> c -> q' -> c' -> QCType q c (B_Endpoint a b) -> QCType q' c' (B_Endpoint a b) -> ErrMsg -> QCType (q, q') (c, c') (B_Endpoint a b) Source # qcdata_promote :: BType (B_Endpoint a b) -> B_Endpoint a b -> ErrMsg -> BType (B_Endpoint a b) Source # | |
| (QCData a, QCData b, QCData c) => QCData (a, b, c) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c) -> m (QCType q' c' (a, b, c)) Source # qcdata_zip :: (a, b, c) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c) -> QCType q' c' (a, b, c) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c) Source # qcdata_promote :: BType (a, b, c) -> (a, b, c) -> ErrMsg -> BType (a, b, c) Source # | |
| (QCData a, QCData b, QCData c, QCData d) => QCData (a, b, c, d) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d) -> m (QCType q' c' (a, b, c, d)) Source # qcdata_zip :: (a, b, c, d) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d) -> QCType q' c' (a, b, c, d) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d) Source # qcdata_promote :: BType (a, b, c, d) -> (a, b, c, d) -> ErrMsg -> BType (a, b, c, d) Source # | |
| (QCData a, QCData b, QCData c, QCData d, QCData e) => QCData (a, b, c, d, e) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d, e) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d, e) -> m (QCType q' c' (a, b, c, d, e)) Source # qcdata_zip :: (a, b, c, d, e) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d, e) -> QCType q' c' (a, b, c, d, e) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d, e) Source # qcdata_promote :: BType (a, b, c, d, e) -> (a, b, c, d, e) -> ErrMsg -> BType (a, b, c, d, e) Source # | |
| (QCData a, QCData b, QCData c, QCData d, QCData e, QCData f) => QCData (a, b, c, d, e, f) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d, e, f) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d, e, f) -> m (QCType q' c' (a, b, c, d, e, f)) Source # qcdata_zip :: (a, b, c, d, e, f) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d, e, f) -> QCType q' c' (a, b, c, d, e, f) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d, e, f) Source # qcdata_promote :: BType (a, b, c, d, e, f) -> (a, b, c, d, e, f) -> ErrMsg -> BType (a, b, c, d, e, f) Source # | |
| (QCData a, QCData b, QCData c, QCData d, QCData e, QCData f, QCData g) => QCData (a, b, c, d, e, f, g) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d, e, f, g) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d, e, f, g) -> m (QCType q' c' (a, b, c, d, e, f, g)) Source # qcdata_zip :: (a, b, c, d, e, f, g) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d, e, f, g) -> QCType q' c' (a, b, c, d, e, f, g) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d, e, f, g) Source # qcdata_promote :: BType (a, b, c, d, e, f, g) -> (a, b, c, d, e, f, g) -> ErrMsg -> BType (a, b, c, d, e, f, g) Source # | |
| (QCData a, QCData b, QCData c, QCData d, QCData e, QCData f, QCData g, QCData h) => QCData (a, b, c, d, e, f, g, h) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d, e, f, g, h) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d, e, f, g, h) -> m (QCType q' c' (a, b, c, d, e, f, g, h)) Source # qcdata_zip :: (a, b, c, d, e, f, g, h) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d, e, f, g, h) -> QCType q' c' (a, b, c, d, e, f, g, h) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d, e, f, g, h) Source # qcdata_promote :: BType (a, b, c, d, e, f, g, h) -> (a, b, c, d, e, f, g, h) -> ErrMsg -> BType (a, b, c, d, e, f, g, h) Source # | |
| (QCData a, QCData b, QCData c, QCData d, QCData e, QCData f, QCData g, QCData h, QCData i) => QCData (a, b, c, d, e, f, g, h, i) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d, e, f, g, h, i) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d, e, f, g, h, i) -> m (QCType q' c' (a, b, c, d, e, f, g, h, i)) Source # qcdata_zip :: (a, b, c, d, e, f, g, h, i) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d, e, f, g, h, i) -> QCType q' c' (a, b, c, d, e, f, g, h, i) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d, e, f, g, h, i) Source # qcdata_promote :: BType (a, b, c, d, e, f, g, h, i) -> (a, b, c, d, e, f, g, h, i) -> ErrMsg -> BType (a, b, c, d, e, f, g, h, i) Source # | |
| (QCData a, QCData b, QCData c, QCData d, QCData e, QCData f, QCData g, QCData h, QCData i, QCData j) => QCData (a, b, c, d, e, f, g, h, i, j) # | |
Defined in Quipper.Internal.QData Methods qcdata_mapM :: Monad m => (a, b, c, d, e, f, g, h, i, j) -> (q -> m q') -> (c0 -> m c') -> QCType q c0 (a, b, c, d, e, f, g, h, i, j) -> m (QCType q' c' (a, b, c, d, e, f, g, h, i, j)) Source # qcdata_zip :: (a, b, c, d, e, f, g, h, i, j) -> q -> c0 -> q' -> c' -> QCType q c0 (a, b, c, d, e, f, g, h, i, j) -> QCType q' c' (a, b, c, d, e, f, g, h, i, j) -> ErrMsg -> QCType (q, q') (c0, c') (a, b, c, d, e, f, g, h, i, j) Source # qcdata_promote :: BType (a, b, c, d, e, f, g, h, i, j) -> (a, b, c, d, e, f, g, h, i, j) -> ErrMsg -> BType (a, b, c, d, e, f, g, h, i, j) Source # | |
type QCDataPlus qc = (QCData qc, QData (QType qc)) Source #
The QCDataPlus type class is almost identical to QCData,
except that it contains one additional piece of information that
allows the type checker to prove the implications
QCDataPlus qc implies QShape (BType qc) (QType qc) (CType qc) QCDataPlus qc implies QData (QType qc) QCDataPlus qc implies CData (CType qc) QCDataPlus qc implies BData (BType qc)
This is sometimes useful, for example, in the context of a function
that inputs a QCData, measures all the qubits, and returns a
CData. However, the additional information for the type checker
comes at a price, which is drastically increased compilation time.
Therefore QCDataPlus should only be used when QCData is
insufficient.
Shape-related operations
Some Quipper functions, such as print_generic, require a
shape parameter. A shape parameter is a parameter passed to a
function for the sole purpose of specifying the type or size of
some data structure, without actually specifying any data.
Example: given a circuit
circuit :: ([Qubit], Bit) -> Circ Qubit,
the command
print_generic Preview circuit ([qubit,qubit,qubit], bit)
tells Quipper to preview the circuit for a problem size of 3 qubits and 1 bit.
A dummy term of type Bit. It can be used in shape parameters
(e.g., qc_init), as well as shape type parameters (e.g.,
qcdata_mapM).
A dummy term of type Qubit. It can be used in shape parameters
(e.g., qc_init), as well as shape type parameters (e.g.,
qcdata_mapM).
qshape :: QData qa => BType qa -> qa Source #
Return a quantum data structure of the given boolean shape, with
every leaf initialized to the undefined dummy value qubit.
qc_false :: QCData qc => qc -> BType qc Source #
Return a boolean data structure of the given shape, with every
leaf initialized to False.
Quantum type classes
Haskell provides many convenient type classes: Eq, Ord, Num, etc.
Quipper provides quantum analogues of some of these.
For instance, Haskell’s Eq a
(==) :: a -> a -> Bool.
Correspondingly, our QEq a qa ca
q_is_equal :: qa -> qa -> Circ (qa,qa,Qubit).
Similarly, where Haskell’s Num class has methods +, *,
signum, the class QNum has
q_add, q_mult,
q_signum, and so on.
(QNum is defined in
Quipper.Libraries.Arith.)
All quantum type classes assume (a) that their instance types are
QCData, and (b) that the corresponding classical parameter types
are instances of the corresponding Haskell type classes.
Quantum type classes are designed to work well with the automatic circuit generation of Quipper.Internal.CircLifting: the methods of Haskell’s standard type classes are translated into their quantum analogues, where available.
type QEq qc = QCData qc Source #
This is a quantum analogue of Haskell’s Eq type class. Default
implementations are provided; by default, equality is bitwise
equality of the underlying data structure. However, specific
instances can provide custom implementations. In this case,
q_is_equal is a minimal complete definition.
class (QEq qa, QData qa) => QOrd qa where Source #
This is a quantum analogue of Haskell's Ord type class. Its
purpose is to define a total ordering on each of its instances. The
functions in this class are assumed dirty in the sense that they do
not uncompute ancillas, and some of the inputs may be returned as
outputs. The functions are also assumed to be non-linear safe,
i.e., they apply no gates to their inputs except as control
sources. Minimal complete definition: q_less or q_greater. The default
implementations of q_max and q_min assume that both arguments
are of the same shape (for example, numbers of the same length).
Minimal complete definition
Nothing
Methods
q_less :: qa -> qa -> Circ Qubit Source #
Test for less than.
q_greater :: qa -> qa -> Circ Qubit Source #
Test for greater than.
q_leq :: qa -> qa -> Circ Qubit Source #
Test for less than or equal.
q_geq :: qa -> qa -> Circ Qubit Source #
Test for greater than or equal.
q_max :: qa -> qa -> Circ qa Source #
Compute the maximum of two values.
q_min :: qa -> qa -> Circ qa Source #
Compute the minimum of two values.