The three main subject areas are (1) Cloud Microphysics (Chapter 6), (2) Convection and Hurricanes (Chapter 8), and (3) the Boundary Layer (Chapter 9).
Quiz 2: Wednesday February 28, 2024
Quiz 3: Wednesday March 27, 2024
The focus will be on the lecture notes up to January 26 on the condensational growth of cloud droplets. Other study material will be Assignments 1 - 3, questions on the Previous Test Questions related to the lecture material (pages 1 - 5), and the sections of the text related to the lecture material. You will be given a copy of the formula sheet with the quiz. It is important to understand how to calculate basic water vapor quantities, such as wv, es, wvs, use of the ideal gas law for the dry air and water vapor components within an air parcel, etc.
The focus will be on the material since the last quiz, starting with the discussion of collision efficiency, and ending with weather radar, and the questions from Assignment 4. and up to page 85 (in the .pdf numbering). This includes precipitation processes, especially the warm rain collision coalescence process and the continuous collection model, evaporation of rain, the Marshal Palmer distribution, and radar. The best strategy is to study questions related to these topics from Previous Test Questions. Useful background material on water vapor and thermodynamics is in Chapter 3.
All lecture notes, assignment questions, and handouts related to ice microphysics, the radar bright band, ice precipitation, convection, convective adjustment, hurricanes (including the storm surge), the surface hydrology comparison between Halifax and Berkeley, and the supplemental material for convection given below.
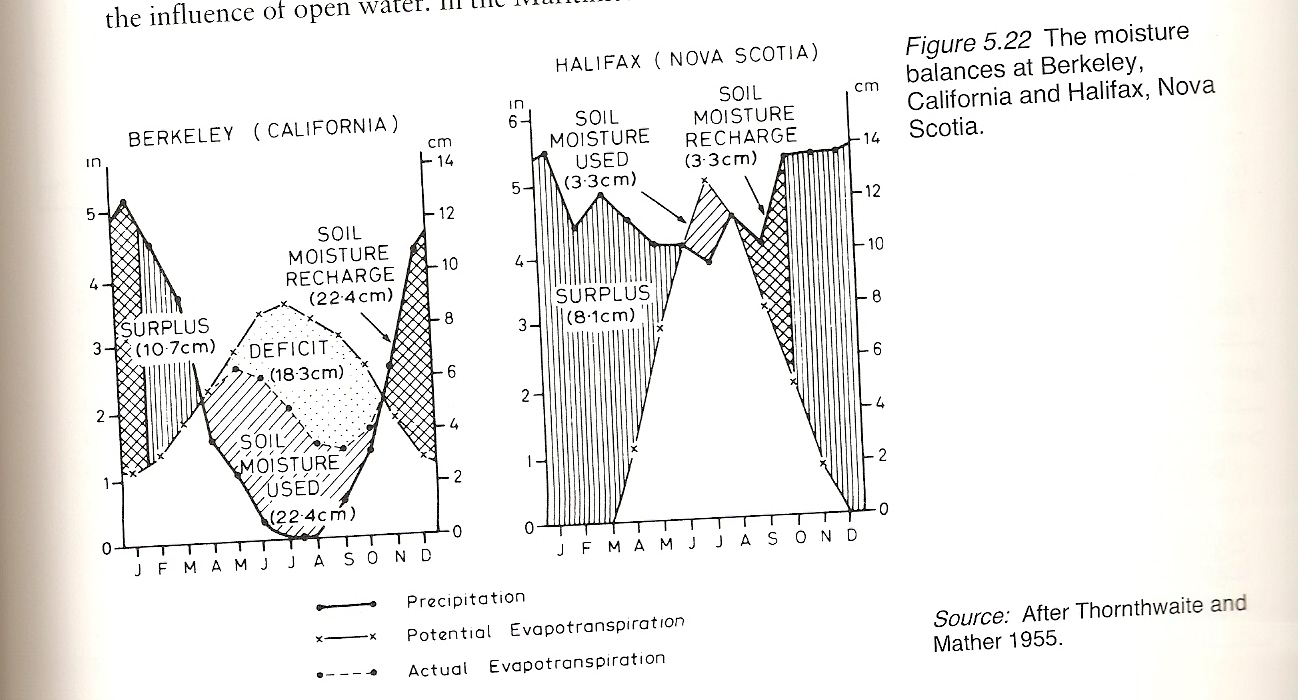
You should know the reasons for the Mediterranean type seasonal variation of rainfall at Berkeley. Also a good climate for growing grapes since they like heat, and have deep roots to access water when the surface soil moisture is low. You should be familiar with the 4 possibilities for rainfall: (i) water runoff to surface waterways when soild moisture is high, (ii) evaporation from the surface, (iii) replenishment of soil moisture, and (iv) replenishment of aquifers. Also should know under what circumstances each is more likely (e.g. that runoff more likely when soil moisture high). Should also know the factors that affect surface evapotranspiration (e.g. downwelling solar radiation, ground temperature, air temperature, vegetation). Also know difference between potential and actual evaporatranspiration.
Students are often asked to calculate, for example, the buoyancy acceleration of an air parcel. If the effects of temperature and water vapor mixing on air parcel density are being taken into account, you need to use the virtual temperature. In this case, the buoyancy acceleration of an air parcel in the cloud is B = (Tv(cloud) - Tv(background air))/Tv(background air). To have two significant digits in B, the relevant virtual temperatures usually have to be calculated to five digits, e.g. Tv(cloud) = 261.59 K. If you were to simply use Tv(cloud) = 262 K, you would not get an accurate answer. The number of significant digits you should retain depends on the problem. When you are taking a difference of two numbers that are very close, it is usually neccessary to retain more digits to get a sensible answer.
You should acquire a familiarity with these topics over the course of the term, if you haven't already. I will also try to give some introduction to these topics where they are discussed in class.
Often in a question you want to find the mass per unit area between two pressure levels p1 and p2. From the hydrostatic relation, dp/g = -ρdz. ρdz has the dimensions of kg/m2, or mass per unit area, so therefore the mass per unit area between the two pressure levels is just dp/g.
(i) Use the CC relation to get es = 6.986 hPa.
(ii) Use the ideal gas law for the dry air component of the air parcel. Make sure to use for the dry pressure pd = p - e = 700 hPa - 6.986 hPa = 693.014 hPa, where e = es from (i) and p is the given total pressure of the air parcel. Should get ρd = 0.878 kg/m3.
(iii) Use the IGL for water vapor. Should get ρv = 0.0055 kg/m3.
(iv) wv = ρv/ρd = 0.00627 kg v/kg dry air.
(v) Use the cloud base temperature to get es = 19.36 hPa. Then use wv = ε(e/(p-e)) = 0.01367.
(vi) wl = wv (at cloud base) - wv (in cloud) = 0.01367 - 0.00627 = 0.00743.
Question 2.
(i) 5555 moles
(ii) 56.9 moles
(iii) Should get e/es = fH2O = NH2O/(NH2O + NX) = 0.98. Here, NX = NNa + NCl = 2NNaCl (i.e. i = 2). Main issue here was not to use i = 2. NaCl dissolves into Na and Cl ions in water.
Question 3.
For T = 25 C, es = 32 hPa, so e = 0.9 x 32 hPa = 28.78 hPa in the atmosphere. The es of the 20 C lake surface is es = 23.45 hPa. Since e (of atm) > es of lake surface, the atmosphere is supersaturated with respect to the cold water surface, and there will be net condensation on to the lake surface. Full marks for quantitative arguments only.
Question 4.
(i) Use the Kohler curve expression for Sc in terms of a and b to get Sc = 0.0385. Note that in the formula for b, Mx stays in g/mole, while mx is in kg. Using i = 2, Mx = 58 g/mole, and mx = 1 x 10-18, I get b = 1.48 x 10-25 m3.
(ii) At steady state, CCN must be on the Kohler curve. Use the Kohler curve expression S = a/r - b/r3. Plug in the values for a, b, and r. Should get S = -0.034, or RH = 0.965.
(iii) You would expect droplet to shrink since RH is being reduced from the equilibrium RH for the starting radius.
Question 5.
As RH goes up, mean CCN size goes up, scattering cross-section goes up and more light is reflected. Note that "activation" in this context is not appropriate, as it refers to the CCN -> cloud droplet transformation only. Haze refers to aerosols that have increased in size due to higher RH, not to CCN that have been activated and created a cloud.
Question 6.
Discussed in Previous Test Questions.
Question 7.
Larger CCN have a smaller Sc, so are more likely to be activated.
Question 8.
Condensational growth results in more rapid growth of the smaller cloud droplets (since dr/dt goes as 1/r), so the cloud droplet size distribution is narrowed.
(i) In the tropics, the potential temperature is roughly 300 K at the surface (assume 1000 hPa) and 345 K at 200 hPa. What is the temperature at 200 hPa?
(ii) Assume that 200 hPa is at 12 km, and that the potential temperature linearly increases with height in the tropics. What is the temperature at 5 km, if the pressure at 5 km is 550 hPa. (Do not assume a scale height for temperature, or that the temperature linearly changes with height.)
(iii) What is the atmospheric density at 5 km? This would technically be the dry air density, since you do not know anything about the relative humidity. (in kg/m3).
(iv) Assume that the upward convective mass flux in the tropics occurs inside convective clouds that occupy a very small area. Assume that convective clouds detrain all of their mass at 200 hPa, and that it takes two weeks for an air parcel to sink to the surface (to 1000 hPa) via radiative cooling. Estimate the (assumed constant) clear sky subsidence rate in the tropics, expressed as a pressure velocity in Pa/s. This would be the total (Lagrangian) derivative dp/dt, or the rate of increase of the parcel pressure as it sinks to the surface. (Hint: sounds complicated but this question is trivial ).
(v) Use the hydrostatic relationship to express the pressure velocity dp/dt in (iv) as a rate of change of height w = dz/dt at 5 km (in which you can approximate the density as a constant). Express your answer in km/day. Note that for a given constant pressure velocity (dp/dt), w will be inversely proportional to density, so larger in the upper troposphere than near the surface. To first order, expressing the subsidence as a constant dp/dt is more realistic than a constant dz/dt. Note that dp/dt and dz/dt are being used as "total derivatives", the rate of change of something following the air parcel motion.
(vi) Estimate the local tendency in potential temperature at 5 km due to subsidence (in K/day) (note: "due to subsidence" in this context means "due to vertical advection"). (Note: in most of the troposphere, temperature decreases with height (dT/dz < 0). If you treat temperature as a conserved quantity, you would then say that descent brings down "cooler" air which leads to a cooling. But this is incorrect. Instead, descent brings down air with higher potential temperature (almost always), which leads to a warming. This subsidence warming is mainly balanced by radiative cooling.)
(vii) Assume that air enters the base of convective clouds from between 1000 hPa and 900 hPa. Estimate the timescale for removal of air from the boundary layer due to convection (express in days). What is the timescale for removal? If I have 10 eggs, and I am giving 1 a day to my friend, in how many days are the eggs all gone? (i.e. timescale for loss = mass/L where L = dm/dt is the loss rate.) You have to assume that the mass in the 1000 - 900 hPa layer is lost mainly through convection, and increased mainly by subsidence. (In reality, over high SST regions low level convergence is an important source of mass to the boundary layer). There is a note above on how to calculate the mass per unit area between two pressure levels.
Question 2.
6.10 from the text (question concerns curvature effect only) Assume that the small droplet is in steady state. Also, retain more than the usual number of digits. The supersaturation is tiny, since you are taking the difference of two terms that are almost equal.
(i) T = 217.2 K
(ii) T = 268.65 K. Use the given height dependence of PT to get PT at 5 km. Then solve for T using PT and pressure. Do not assume that p decreases with altitude with a constant scale height. That is valid only in an isothermal atmosphere.
(iii) ρ = 0.7132 kg/m3. Find the density from the local temperature and pressure. Do not use a scale height. That gives only an approximate answer.
(iv) ω = 0.066 Pa/s. 800 hPa divided by 2 weeks.
(v) dz/dt = -0.8216 km/day. Use dp = - ρgdz. Divide through by dt and assume ρ is constant.
(vi) dθ/dt = 3.06 K/day. Treat θ as a conserved quantity that is advected downward by the vertical wind, so dθ/dt = -dz/dt * dθ/dz.
(vii) This is a mass conservation problem. There are three terms to the mass budget of the boundary layer: (i) downward subsidence of ω = 0.066 Pa/s (or 57 hPa/day), (ii) convective removal, and (iii) divergence from the horizontal wind (can be positive or negative). If (iii) is zero, then (i) and (ii) must balance. Note that mass is proportial to pressure. Therefore 57 hPa per day must be removed from the 900-1000 hPa layer every day by convection. This corresponds to a timescale of 100/57 = 1.75 days. Note here that a loss timescale is equal to mass divided by loss rate.
Answer to Question 2.
6.10. The main issue is to not convert e/es = 1.006 to e/es = 1.01. This is the same as going from S = 0.006 to S = 0.01, and introduces almost a factor of two error.
Use the simplified dilute limit version of the Kohler curve given in the notes to derive expressions for the critical radius rc and critical supersaturation Sc in terms of the parameters a and b (i.e. prove what was given in the notes).
Question 2.
6.11 from the text. But rather than using the figure to find the answers, use the simplified dilute limit Kohler curve in terms of a and b for parts (a) and (b), and for part (c) use the associated expressions for (b), indicate your values for a and b using MKS units (i.e. kg for mass) rcrit and Scrit from the notes. For parts (a) and Compare your calculations with Figure 6.3. You should not expect complete agreement, because the curves in Fig 6.3 would have been obtained from more accurate expressions. Assume T = 273.15 K, and use the simplified expressions for a and b given in the notes. Part (a) involves some trial and error to find r. If you get two positive solutions for r, pick the one that is stable. To find i in (c), assume that ammonium sulphate totally dissociates in water.
6.11 (a) Should get a = 1.24E(-9) and b = 1.47E(-22). There seem to be 2 answers for positive r: r = 1.08E(-6) m and r = 0.44(-6) m. Probably the stable answer is the smaller r. In general, there are three solutions to a cubic polynomial. Note i = 2 for salt, and watch units (need kg consistency). Need to solve e/es = 1 + a/r - b/r3, where e/es = 1.001. So solve 0.001 = a/r - b/r3, by guessing a number of values for r and seeing what gives the smallest error. Note that you cannot eliminate the a or b term. In this case, there would be no critical rc: need both the curvature effect and the solute effect. You also can't use the formulas for the critical radius rc in terms of a and b: these are valid at the peak in the S curve only.
6.11 (b) Should get a = 1.2E(-9) and b = 9.9E(-24), and e/es = 0.88. Note i = 3. Plug in a, b, and r to get e/es. There is no need to neglect the a or b terms.
6.11 (c) Using above values of a and b, and the expression for Sc, gives Sc = 0.0051.
Look at the question in the "Condensational Growth - Math Questions" of the Previous Test Questions given above on page 5. Do parts (ii) and (iii) (involving condensational heating of cloud droplets).
Question 2.
An aircraft is flying through a cloud at a temperature of T = 260 K and pressure p = 600 hPa. The air in the cloud is saturated (i.e. e = es(T)). Adopt a simplified model of a cloud in which all air parcels enter the cloud at cloud base where the temperature is Tb = 280 K, the pressure is pb = 800 hPa, and that all air parcels in the cloud rise without experiencing precipitation or mixing.
(i) Estimate the total water mass mixing ratio wt at cloud base.
(ii) Estimate the liquid water mass mixing ratio wl measured by the aircraft.
Condensational Growth Question From the Previous Test Questions. Part (ii) is quite straightforward. The main problem in (iii) is finding ρv(∞) - the background water vapor mass density in the cloud. First find es from T. Then use this vapor pressure, and the given temperature, in the the Ideal Gas law for water vapor (i.e. using Rv). You should get ρv(∞) = 0.0055 kg/m3, and a final answer dT/dt = 2.68 K/s. A common problem here was to use the total pressure p instead of the vapor pressure e in finding ρv(∞). It is extremely important, when using the ideal gas law for water vapor, to use the vapor pressure e and not the total pressure. Another issue is that, technically, ρv(∞) in the cloud should be determined from S = 0.005, or RH = 1.005, so that e ends up being 1.005*es. This would give a slightly more accurate result. Many people assumed made the assumption ρd = 1.225 kg/m3. I am not sure where this assumption comes from. However, you do not have to make any assumption on the dry gas density to determine ρv(∞).
Answer to Question 2.
(i) The key here is to recognize that, at cloud base, there is zero cloud condensate, and that the air is saturated, so that wt = wvs. You can define wvs in terms of es, and determine es from the temperature. Should get wt = 0.00714.
(ii) Use the wt determined in (i). Assume this is constant as the parcel rises. Calculate wvs using the local cloud temperature. Then wl = wt - wvs. Should get wl = 0.0055
6.23 of text (continuous collection model)
Question 2.
6.24 of text (evaporating raindrop)
Question 3.
What is the heating rate dT/dt of a 10 micron radius supercooled cloud droplet with T = 260 K due to long wave (thermal) emission? Assume liquid water is a black body surface. The rate of heating will be negative (i.e. a cooling). As a first step, you may want to solve for the cooling rate for general radius (i.e. similar to the expression for the dT/dt due to condensational heating in the previous assignment.) You get a very fast rate of cooling. Keep in mind that, within a cloud, the actual cooling rate will be smaller due to absorption of radiation from neighboring cloud droplets. However, near the cloud edges, this absorption is reduced, so cooling from emission will ordinarilly dominate.
Question 4.
A cloud droplet starts off at cloud base with a radius of 20 microns. The cloud has a constant upward vertical velocity of 1 m/s. The fall speed of the cloud droplet is given by v1(r) = k3 r, where where k3 = 6000 /s. Assume the the collection efficiency E = 0.8, and that the Liquid Water Content LWC = 2 g/m3.
(i) What is the size of the cloud droplet at its highest altitude?
(ii) How high above cloud base is the droplet at this point?
(iii) How long does it take for the droplet to reach this highest altitude from cloud base?
(iv) Use the implicit expression derived in class to estimate the radius of the drop when it exits the cloud. You can only solve implicit expression by trial and error. You need to show a reasonable amount of the work that you made to find a solution with a reasonable error.
6.23 from the text. First determine the LWC (i.e. liquid water density) from the droplet size and number density. Then use v1 = k3 r1 (with k3 = 6000 /s) in dr1/dt = (v1 LWC E)/ (4 ρw) to get dr1/dt = C r1, where C is a collection of constants. Rewrite as dr1/r1 = C dt. Integrate using the given initial and final r1, and solve for the elapsed time. Should get 1.27 hours.
Answer to Question 2.
6.24 (i) from the text. Since e/es = 0.6, S = -0.4. Use r (dr/dt) = Gl S. This can be re-written r (dr/dz) (dz/dt) = Gl S. (A good trick to remember) Use dz/dt = v = 6000 /s r (as above). This gives r (dr/dz) r = C, where again C is a bunch of constants. Integrate r2 dr = C dz to get a relationship between the initial radius ri, final radius rf, and H, the height that the raindrop fell. You are given ri and H. Use to solve for rf. Should get r = 0.67 mm.
6.24 (ii) from the text. What is the time it takes to fall 5 km? Go back to r dr = Gl S dt. Integrate and use your solution for rf from (i) to solve for the time. Should get t = 985 s.
Answer to Question 3.
Start from dQ = cwm dT, where cw is the specific heat of the droplet, dQ is the heat added, and dT is the change in temperature, and m is the mass. This gives, (dT/dt)cwm = dQ/dt. dQ/dt is the rate of energy loss due to LW emission σT4 multiplied by the area of the droplet, 4πr2. Use this to solve for dT/dt. You should get about -18.4 K/s. This is incredibly fast, of course. The cooling rate dT/dt will decrease with increasing r. This is one of the reasons why you tend to have only larger animals in the Arctic. Small animals lose heat too fast in the winter (both by radiation and thermal diffusion) relative to their heat capacity to survive. Similarly, it is more energy efficient to live in an apartment building than a small house, because apartment buildings have a smaller surface area to volume ratio.
Answer to Question 4.
(i) 167 microns
(ii) 516 m
(iii) Should get about 881 s = 14.7 min. Use dr/dt = (v*LWC*Ec)/(4*ρw). Express v in terms of r. Collect dr/r term on LHS and integrate both sides. Do not treat the velocity v of the cloud droplet as a constant.
(iv) Should get around 580 microns by trial and error.
A droplet of supercooled water at -15 C starts to freeze. Assume the final temperature of the remaining water and ice is 0 C. What fraction of of the original water is frozen (fraction by mass). Assume that the droplet does not exchange heat with its environment.
Question 2.
6.27 from the text, involving condensational growth of an ice crystal in a water saturated environment. Use the version of Eq. 6.37 discussed in the notes for a circular disk. DO NOT use Figure 6.39. You can assume the diffusion constant D = 21.2 x 10-6 m2/s. Assume a pressure p = 500 hPa. Note that a water saturated environment means a mixed phase cloud. You have to make some assumption on the initial radius of the ice crystal. The easiest assumption is to assume that the initial radius is zero. To solve, express the mass in terms of radius (for a disk) and integrate over radius.
Please show the following intermediate answers:
(i) The Si in the cloud.
(ii) The ρv(∞) in the cloud. Keep in mind, ρv(∞) is nothing other than the background water vapor density inside the cloud. I am stuck with using this variable because that is what the text uses, but it is always confusing to students.
(iii) What is the radius after 30 minutes?
(iv) What is the mass after 30 minutes?
The specific enthalpy of water can be defined hl(T) = hl0 + cl*T, where hl0 is the specific enthalpy of water at 0 C, and T is therefore in C. Similarly, one can define hi(T) = hi0 + ci*T for ice. Note that lf = hl0 - hi0, where lf is the latent heat of fusion at 0 C. There is no external heating in this question so the initial and final enthalpies are equal: Hi = Hf. Here, we have only water in the beginning with mass M, so the initial enthalp is Hi = hl(-15 C)*M. Using hl(T) = hl0 + cl*T, we have Hi = hl0*M - 15*cl*M. We have some combination of ice and water at 0 C in the end. Assume that f is the fraction frozen. Then the final enthalpy Hf is a combination of the enthalpies of liquid water and ice at 0 C: Hf = (1-f)*hl0*M + f*hi0*M. Setting Hi = Hf, and canceling out M on both sides gives, hl0 - 15*cl = (1-f)*hl0 + f*hi0. Dropping the hl0 on both sides gives: -15*cl = -f*hl0 + f*hi0. This can be written: f = 15*cl/(hl0 - hi0). Remember that lf = hl0 - hi0 (Remember that here lf would refer to lf at 0 C only!). This gives: f = 15*cl/lf = 0.19. Note that the book refers to the specific heat of water as cw, but I prefer cl.
Answer to Question 2.
(i) First calculate es and esi at -5 C. You need this to find Si. You should get Si = 0.046.
(ii) You also need es to find ρv(∞), the background water vapor density of the cloud. Use the ideal gas law for water vapor es = ρv(∞) RvT, with es the saturated water vapor pressure for -5 C. You should get ρv(∞) = 3.38E-03 kg/m3.
(iii) Use the given value for D to find Gi. You should find GiSi = 3.2E-09 kg/sm. You can easily show dm/dt = 8rGiSi from the notes for a disk. The expression for m(r) of a disk with constant thickness h is m(r) = πρir2. Take d/dt of both sides to express dm/dt in terms of dr/dt. You should get dr/dt = 4GiSi/πhρi. Integrate over time to find the change in r, starting from r = 0. This is a trivial integration since dr and dt are the only variables. You should get that the final radius rf = 0.796 mm
(iv) The final mass mf = 1.8E-08 kg.
6.28 from the text. Growth of an ice crystal by riming. Use 6.26 with v2 = 0 and v1 expressed in terms of M as given. Assume that r1 is fixed at 0.5 mm. You know the initial mass, the final mass, and Ec. You use the given relationship between v1 and M, and integrate over M to find the time difference. It is probably easiest to convert all mass units to mg. (Next time: this is actually a bit of a strange question. There is a transition from a disk to spherical geometry, so no right way to treat analytically. Here, the process is treated like warm rain collection, but just with a different relationship between mass and terminal velocity to account for the "sponginess" of graupel. But even though the mass is increasing, the surface area for droplet collection is strangely assumed fixed - at least I don't see any other way of doing the question without a given M-r relationship for graupel. The only other option would likely be to assume spherical geometry throughout.) Watch units. Since the formula for fall speed is given in mg, it is probably easiest to convert all masses to mg, including of course the initial and final masses, and the given LWC. You should get about 169 s. The point of this calculation is to show that graupel can grow quite quickly.
Question 2.
(i) A glass of pure water 20 cm deep at 20 C is sitting on a table. A thin layer at the top is cooled to 0 C by an ice cube. Estimate the maximum downward velocity the cold 0 C water would have at the bottom of the glass if it sank to the bottom of the glass without mixing. The density of pure water is 999.8395 kg/m3 at 0 C and 998.2071 kg/m3 at 20 C (from Wikipedia). Remember that in the calculation of buoyancy acceleration, you are taking a small difference between two large terms that are almost equal, so need to retain enough digits to get an accurate answer. Hint: according to Archimedes, the buoyancy acceleration B of an object is equal to the density of the fluid the object is floating in, minus the density of the object itself, normalized by the density of the fluid, times g. With this definition B > 0 refers to upward accelerations.
(ii) Suppose the layer of 0 C water was 1 mm thick. What is the change in gravitational potential energy between the initial and final water configurations? (i.e. between the configuration with the 0 C water sitting on top of the warm water, and with the layer of cold water sitting at the bottom). Assume the radius of the glass is 10 cm. Note that it is important here to retain at least 4 significant digits in your answer, since taking the difference between two large terms.
(iii) Would you expect this change in gravitational energy of the system to equal the increase in kinetic energy of the cold water as it falls to the bottom? Why or why not?
Use the density of graupel, the final spherical shape, and the final radius, to find the final mass mf. Should get mf = 0.05236 mg. Then do the integral. Answers with a similar approach include 168 s, 188 s, 177 s, 151 s, to 210 s, with 177 s being the most common, and likely most correct. Note that the speed of the graupel V1 is dependent on the graupel mass M, so should be part of the M integral. You can't just ignore the dependence of V1 on mass, and just plus in the value of final mass at the end. Doing this seems to give t = 151 s.
Answer to Question 2.
(i) B = -0.016 m/s2. Use vf2 = v02 + 2hB, and v0 = 0, to get vf = 0.08 m/s. Or, since the integrated buoyancy work is equal to net work per unit mass, can just set B times vertical distance equal to 0.5 times v squared.
(ii) The mass of the cold water is Mc = (0.001 m)π(0.1 m)*(0.1 m)*(999.8395 kg/m3) = 0.0314 kg. The mass of the warm water is Mw = (0.199 m)π(0.1 m)*(0.1 m)*(998.2071 kg/m3) = 6.2405 kg. The warm water rises by 1 mm, so increases its gravitational potential energy by Mw*(0.001 m)*g = 0.06115 J. The cold water sinks by 0.199 m, so decreases its gravitational potential energy by Mc*(0.199 m)*g = 0.06124 J. The decrease is larger than the increase, so NET CHANGE IN GPE = 0.06115 J - 0.06124 J = - 9.0E-05 J. Note that because the difference in the density of the warm and cold water is tiny, the net change in GPE is small.
(iii) The KE acquired by the sinking of the cold layer = 0.5*Mc*v*v = 1.0E-04 J. During this vertical turnover, the warm water feels an upward buoyancy acceleration, and will acquire an upward velocity, and a non-zero kinetic energy. However, it turns out that because of the mass difference, the speed acquired by the thin cold layer is larger than the warm layer, so that the kinetic energy acquired by cold water is much larger than the kinetic energy acquired by the warm water. You should have the sum of the two KE's plus the change in GPE equal 0 (conservation of energy), KEw + KEc + dGPE = 0. I have have slightly non-zero residual (even with ignoring KEw), so must be some rounding error.
Assume that a cloudy parcel has T = 275 K and liquid water mass mixing ratio wl = 1.5 g/kg. The background atmosphere outside the cloud has T = 274 K, and relative humidity RH = 0.6. Assume that the total pressure (i.e. pd + e) both inside and outside the cloud is p = 600 hPa. However, note that pd in the cloud is different from pd outside the cloud, and similarly for e. The presence of condensate does not directly affect the pressure in a cloud. However, because it adds to the total density, it does affect pressure indirectly through the hydrostatic equation. For example, within a cloudy parcel, the pressure difference between the top and bottom is increased due to the mass of the condensate. Remember that you must retain enough figures to get an accurate answer for the buoyancy - it is a tiny difference of big numbers. This is especially important for the largest contributor to the total density, usually the dry air density.
(i) What is the water vapor pressure e in the cloud?
(ii) What is the dry air pressure pd in the cloud?
(iii) What is the dry air density ρd in the cloud?
(iv) What is the vapor density ρv in the cloud?
(v) What is the liquid water density ρl in the cloud?
(vi) What is the total density of the air in the cloud (due to dry air, water vapor, and condensate)? Carry enough significant digits that ALL contributions are included.
(vii) What is the vapor density ρv outside the cloud?
(viii) What is the total density of the air in the background atmosphere (due to dry air and water vapor)? Carry enough significant digits that ALL contributions are included.
(ix) What is the buoyancy of the cloudy parcel? (Remember to carry an appropriate number of digits.)
Question 2.
Look at the website http://www.weathergraphics.com/tim/af447/ . Read Section 2. Meteorological analysis.
(i) What is the pressure of the Level of Neutral Buoyancy in Figure 9? The figure was easier to read if I clicked on it. Convert feet to km.
(ii) Estimate the buoyancy at 30000 feet in Figure 9. Only worry about the effect of temperature on buoyancy. You need to learn how to read the temperature from these types of charts.
(iii) What is the maximum undilute updraft velocity for this value of CAPE, in m/s, given the CAPE in Figure 9? Also using the given CIN, what would be the upward motion at the surface required to reach the LFC?
(iv) Do you think aircraft icing played a role in the crash? Why or why not?
(i) 6.986 hPa
(ii) 593.1 hPa
(iii) 0.751 kg/m3
(iv) 0.0055 kg/m3
(v) 0.00113 kg/m3
(vi) 0.7579 kg/m3
(vii) 0.00308 kg/m3
(viii) 0.7611 kg/m3
(ix) 0.04 m/s2
A hurricane is developing at 10 degrees latitude in the Northern Hemisphere. Assume that the rain associated with the hurricane has a constant value of 20 mm/day. Assume that the surface pressure inside the hurricane is 950 hPa, and is not changing. The hurricane is circular with a constant radius of 50 km.
(i) Assume that the rain is produced by the vertical ascent of the air that originates between the surface (fixed at 950 hPa) and 900 hPa. Assume that the air in this layer has a mean total pressure of 925 hPa, a temperature of 27 C, and a relative humidity of 0.8. What is the water vapor mixing ratio wv of this air? (should get wv = 0.0202)
(ii) Assume that, as air from the surface layer rises within the hurricane, ALL of the water vapor is converted into rainfall (Note: in reality some of the initial water vapor will become detrained condensate or water vapor, or become rainfall, and then evaporate, so the fractional percent efficiency for rainfall production is likely closer to 50 percent). Also assume that the total water of the hurricane is constant, and that there is no horizontal exchange of water with the background atmosphere (i.e. that the only water source is evaporation from the ocean). What upward total mass flux (vapor + dry air) from the surface layer in the hurricane (in kg/m2s) is required to produce the mean rainfall rate? [Hint: upward water mass flux at the top of the boundary layer = wv*(upward dry mass flux at the top of the boundary layer) = -1*(downward water flux from rain)]. (Should get around 0.0117 kg/m2s)
(iii) What is the pressure tendency ω due to the vertical motion of the air at the top of the surface layer? I.e. how quickly would the pressure of a rising air parcel decrease as it rises? Assume that pressure levels are fixed in height. (Hint: pressure tendency and mass flux are directly related so the answer is almost trivial. Should get ω = -0.115 Pa/s. Note that upward motion has negative ω.)
(iv) Estimate the divergence in the surface layer of the hurricane. Note that ω at the surface is given as zero. Use the expression for mass conservation in the text, (7.39b) (Should get DIV = -2.3E-05 /s. Note that a negative value of the divergence is called a convergence.)
(v) Assume that the hurricane started from air that was originally motionless. What was the initial value of the absolute vorticity of this air? (should get η = 2.53E-05/s).
(vi) Suppose that the hurricane exists for 2 days, and that the only term in the vorticity budget of the hurricane is the divergence term. What would be the absolute vorticity of the surface layer of the hurricane at the end of 2 days? (The divergence in the surface layer is constant as calculated above.) You should get exponential growth in the vorticity with a value η = 1.23E-03 /s after two days.
(vii) Assume that the horizontal flow in the surface layer is pure solid body rotation. In this case, ξ and rotation rate are related via Equation (7.1) in the text. Estimate the horizontal tangential speed of the surface layer at the outer edge of the hurricane (i.e. at a distance 50 km from its center.) You should get about 30 m/s, or about 110 km/hour (not quite hurricane strength actually).
Question 2.
8.12 from the text. (For clarity: 8.6 calculates the pressure deficit at r = 0. Want pressure deficit at r = r0.) It is important to know how to use cyclostrophic balance. It is like Gradient Wind Balance, but without the Coriolis acceleration. Would also be the relevant balance stirring a bowl of soup. It is easy to show that the Coriolis acceleration could be included but would make no difference, since it is much smaller than the other accelerations in this case.
(i) 50 mm of rain in one day over 1 m2 is 50 kg. Call this Mr.
(ii) We are looking for the mass of snow Ms it can melt by cooling from 10 C to 0C.
Let hl(10C) be the specific enthalpy of water at 10 C.
Let hi(0C) be the specific enthalpy of ice at 10 C.
Then starting from conservation of enthalpy:
Hi = Hf
Mw*hl(10C) + Ms*hi(0C) = Mw*hl(0C) + Ms*hl(0C)
Ms*[hl(0C) - hi(0C)] = Mw*[hl(10C) - hl(0C)]
Ms*lf(0C) = Mw*[hl0 + cl*(10C-T0) - hl0 - cl(-T0)]
Ms*lf(0C) = Mw*[cl*10C]
Ms = Mw*4219*10/3.34*10(5)
Ms = 6.32 kg
Answer to Question 9.
(i) Use CC relation for T = 275 K es = 6.986 hPa.
Use IGL for water vapor to get rho_v = 5.5E-3 kg/m3
(ii) pd = p - e = 693.014 hPa Then use IGL for dry air. rho_d = 0.8811 kg/m3.
(iii) rho_l = wl*rho_d = 0.00176 kg/m3
(iv) This part is fairly involved.
Outside the cloud, T = 274 K and p = 700 hPa.
First find e using RH = 0.5 and the CC relation to get es.
e = 0.5*es(274) = 0.5*6.5 hPa = 3.25 hPa.
Then use the IGL for water vapor to get rho_v = 2.57E(-3) kg/m3
To get the dry air density, use pd = p - e = 700 hPa - 3.25 hPa = 696.75 hPa.
Then use the IGL for dry air to get rho_d = 0.8859 kg/m3
In general the total density rho_t = rho_d + rho_v + rho_l.
However, outside the cloud rho_l = 0.
so rho_t = rho_d + rho_v = 0.8859 kg/m3 + 0.00257 kg/m3 = 0.88847 kg/m3
(v) To find the buoyancy, you have to take the difference of the two total densities, with the density of the air outside the cloud, minus the density of the air in the cloud. Note that the signs must make sense. B should be positive when the density of the air outside the cloud is larger than the density of the air inside the cloud.
The total density in the cloud is rh_c = rh_d + rh_v + rho_l = 0.8811 kg/m3 + 0.0055 kg/m3 + 0.00176 kg/m3 = 0.88836 kg/m3
B = g*(rho_b - rho_c)/rho_b = g*(0.88847 - 0.88836)/0.88836 = 0.001 m/s2
Note that typically the buoyancies in clouds are very small since density differences are very small. To get a reasonable answer you must retain quite a few significant figures.